地震動研究支援
近年の地震観測網の発達により、地震観測記録が多く得られるようになりました。大きな地震には特徴的な現象があり、貴重な観測記録が得られています。
例えば、2011年東北地方太平洋沖地震は近代的な観測網が整備されて以降、国内最大規模の地震でした。2016年熊本地震では既知の活断層の一部が活動しましたが、約28時間の間を空けて2度の震度7が観測されました。記憶に新しい2024年能登半島地震では、大規模な地盤の隆起が観測されました。
このような豊富な地震観測記録を防災・減災のために活用することは重要です。
構造計画研究所では建築・土木分野において、長年に渡って地震観測記録の分析や地震動評価手法の高度化に取り組んでいます。本ページではその一端をご紹介します。
地震動研究 取組概要
構造計画研究所は官民の研究機関と共同で最先端の研究活動を行っています。
近年は物理モデルをベースとした「モデル駆動アプローチ」に加えて、データに基づく「データ駆動アプローチ」にも精力的に取り組んでいます。
目次
モデル駆動アプローチ 事例
震源特性研究(特性化震源モデルの高度化)
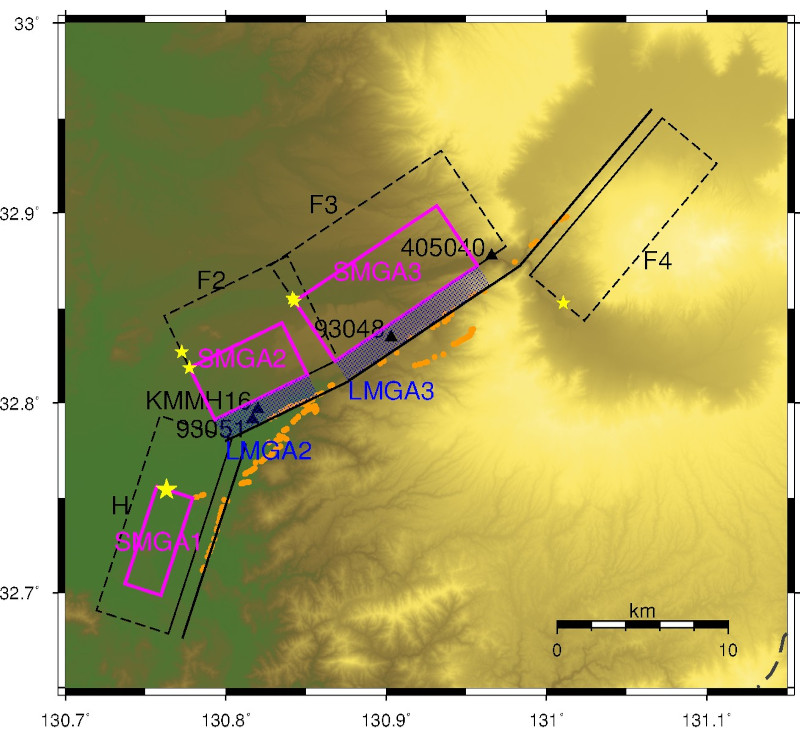
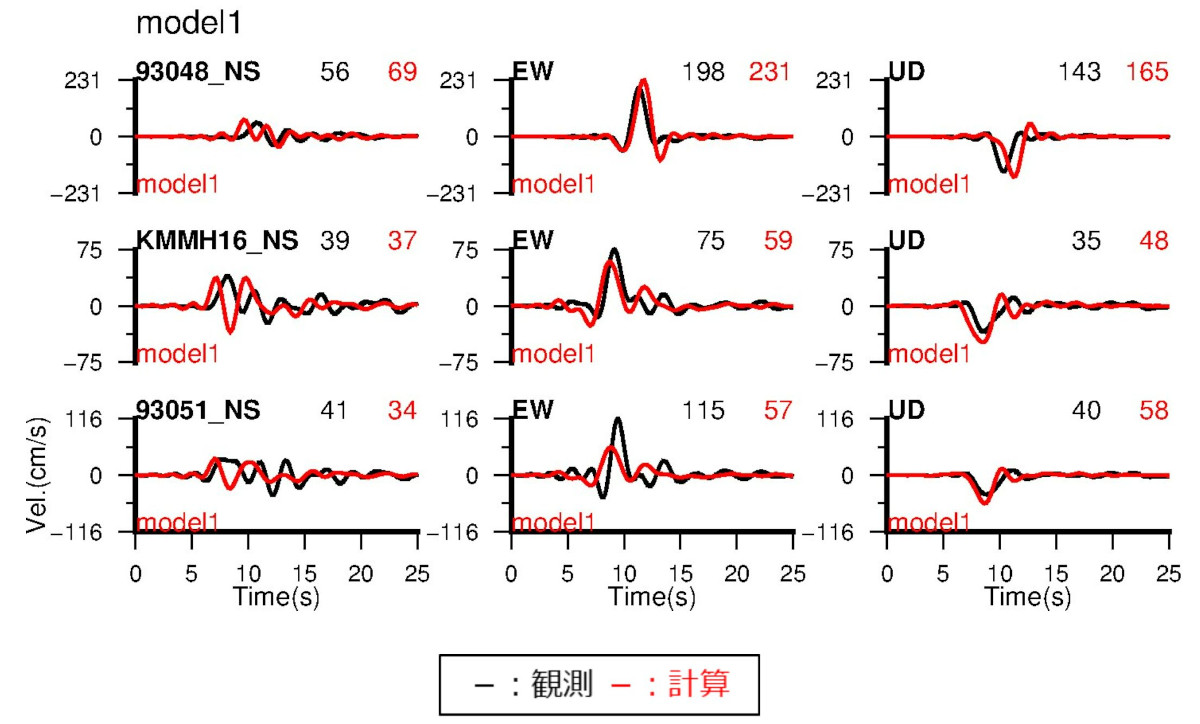
2016年熊本地震では地表に地震断層が現れ、その近傍では貴重な強震動記録が観測されました。具体的には、地震による揺れに加えて、断層の動きによる永久変位も含む記録でした。
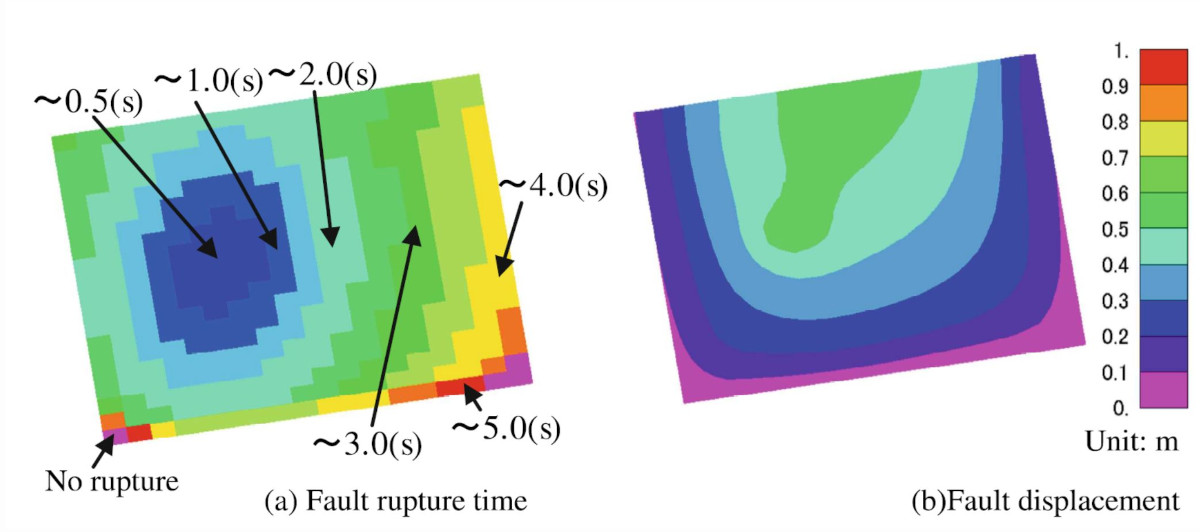
このような震源断層近傍の観測記録を分析し、再現解析を行いました。その結果、震源断層に近い領域に対する地震動評価には、従来の考え方(※1)による地震発生層内の断層のみではなく、地震発生層より浅い部分(浅部断層)もモデル化する必要性を示しました(※2)
※1:地震調査研究推進本部の強震動予測手法(いわゆる「レシピ」)では、震源断層のモデル化範囲は地表から深さ数km程度より深い地震発生層内を対象にしています。
※2:松元康広・宮腰研・高浜勉,2018,2016年熊本地震(Mj7.3)の永久変位を含む長周期(2秒以上)地震動評価のための特性化震源モデルの設定,第15回地震工学シンポジウム,PS1-01-17
動力学的破壊シミュレーション
地震発生時の地下構造物の健全性評価には、断層運動による地表付近の変形量の評価が必要です。
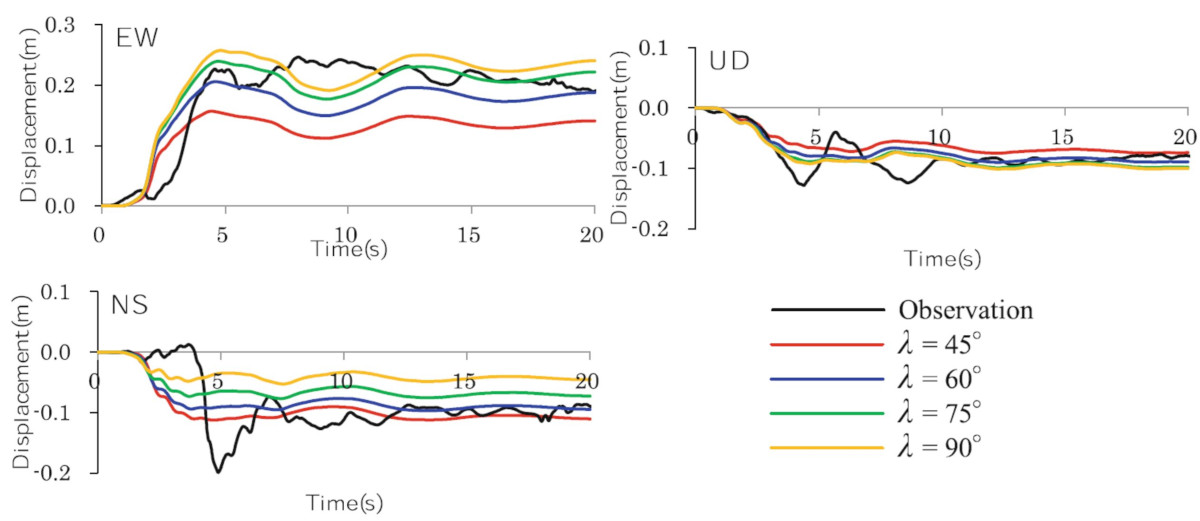
構造計画研究所は、断層変位が地表に現れた2014年長野県北部の地震を対象に、非線形有限要素法による動力学的破壊シミュレーションを実施し、観測された地表地震断層の変位量や断層近傍の観測記録(変位波形)を再現しました(※3)
※3:Yuta Mitsuhashi, Gaku Hashimoto, Hiroshi Okuda and Fujio Uchiyama, Fault Displacement Simulation Analysis of the Kamishiro Fault Earthquake in Nagano Prefecture Using the Parallel Finite Element Method, Model Design and Simulation Analysis, Communications in Computer and Information Science 603, pp. 102-109, 2016.
断層変位による地中構造物への影響評価
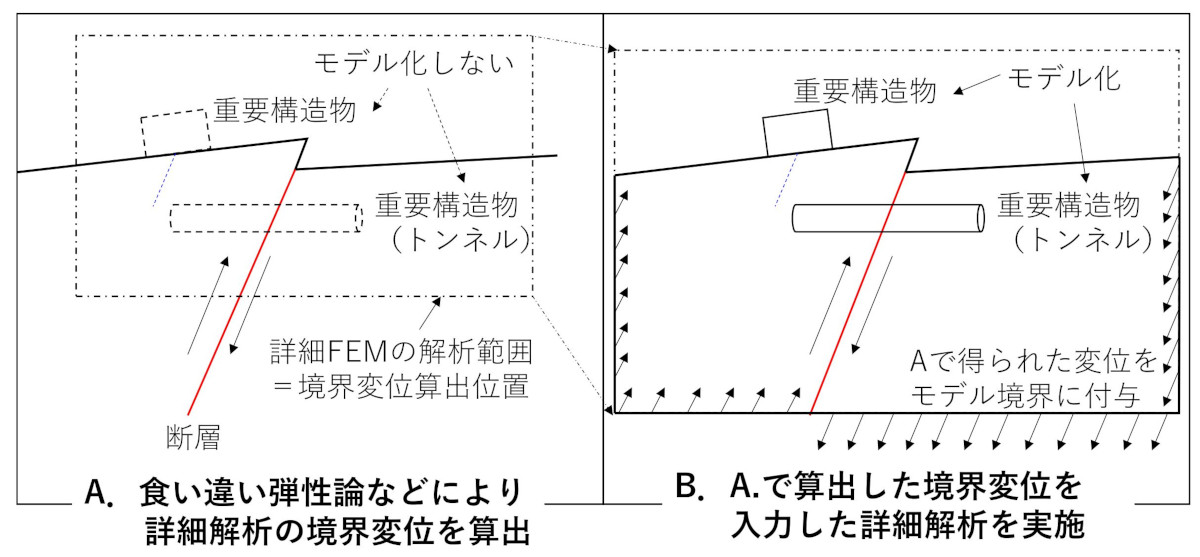
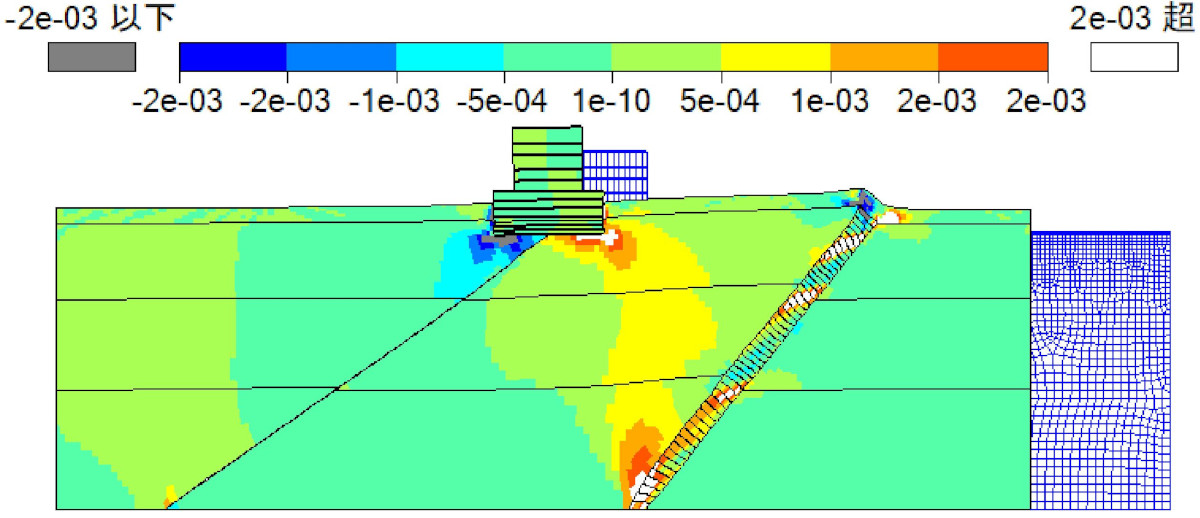
前述のような断層運動により生じた地盤変位に引きずられる形で、震源断層に直接繋がっていない断層(副断層)や破砕帯に変形が生じる可能性も指摘されています。このような現象を評価する手法として、下図に示すように2段階で検討する方法があります。構造計画研究所では手法の適用性・高度化に向けた検討を行っています(※4)
STEP-A:広域な地盤変形量の評価
震源断層による地盤変形量を食い違い弾性論などによって求める
STEP-B:詳細な評価
STEP-Aで求めた地盤変形量を構造物、基礎地盤などを含む詳細なモデルの境界に入力し影響を評価する
※4:三橋祐太・土屋敬人・與猶竜, 2023, 主断層の活動による地殻変動に起因する破砕帯変位量に関するパラメータ解析, 第16回日本地震工学シンポジウム
床応答スペクトルの算定
やや実務よりですが、原子力分野における設備、機器、配管設計のモーダル解析に必要な包絡スペクトルの作成を行っています。
具体的には、
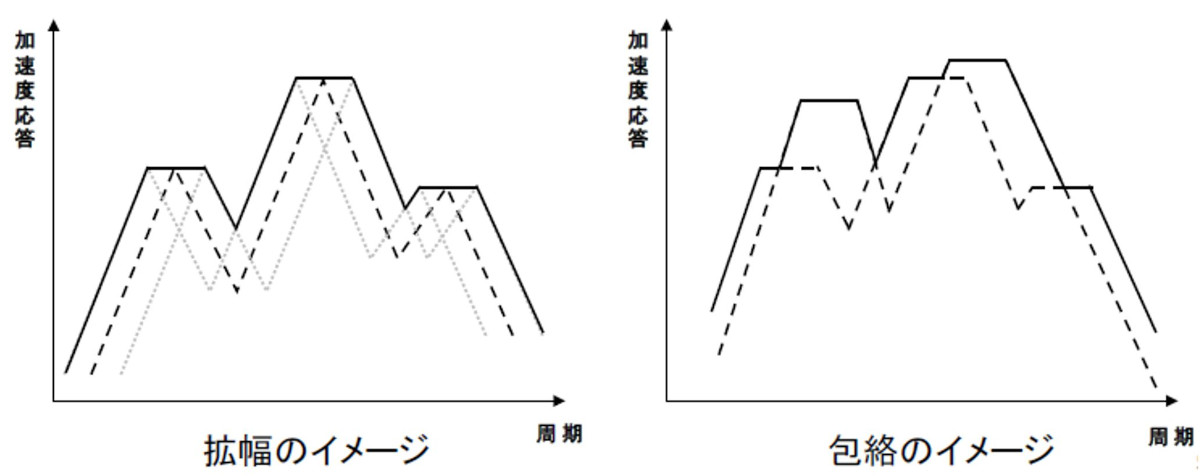
- 床応答スペクトルの作成
- 拡幅スペクトル作成
- 包絡スペクトル作成
- 各種資料の作成
などを行います。
国の審査で十分な実績のある自社開発プログラム(k-WAVE)を用いてお客様の実務支援を行っています。大量ケースのバッチ処理や高度な品質保証にも対応しています。
データ駆動アプローチ 事例
地震動の地域性分析・地震動予測式の開発
豊富な観測記録を整理・分析することで、少数パラメータと少ない計算コストで一定の精度を持つ地震動予測式を構築できます。地震動予測式は多地点の計算や、様々な不確実性を考慮した確率論的な評価に適しています。
幅広い計算条件やいろいろな地域に対し一定の予測精度を発揮しようとすると、単純に観測記録を統計処理し定式化するだけでは不十分です。物理的な背景を踏まえて観測記録を丁寧に分析することが重要です。
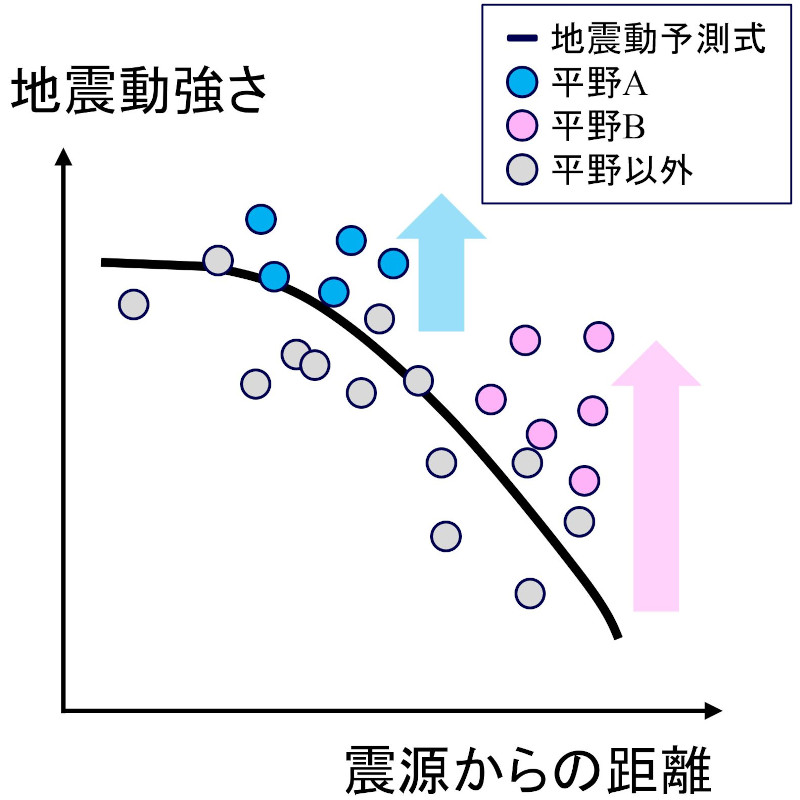
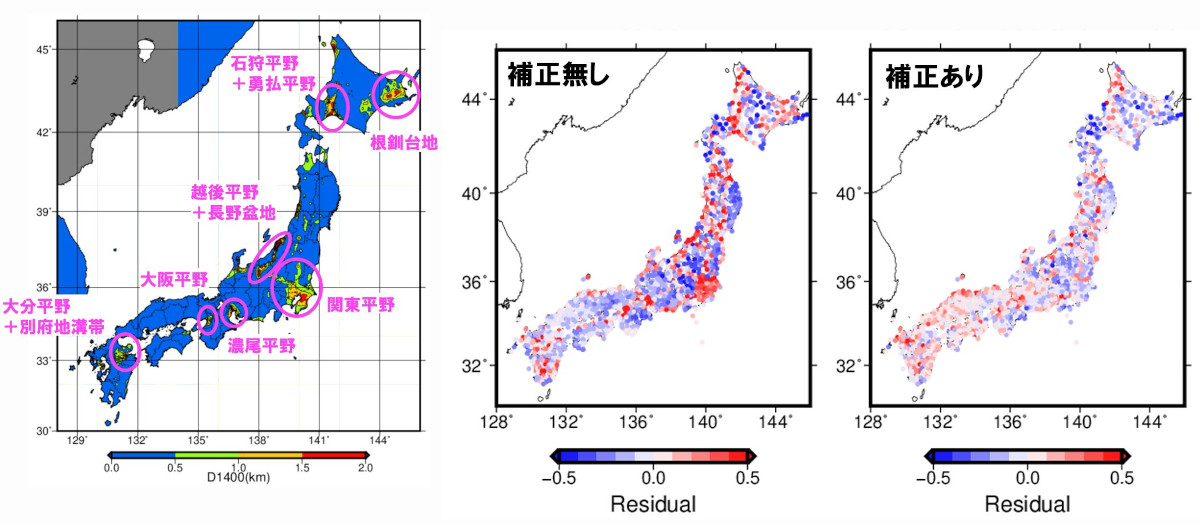
平野毎の地震動増幅特性の違いに着目した検討例を示します。観測記録の回帰分析を行い、基本的な定式化で構築した地震動予測式と、地点ごとの観測記録の残差を検討しました。下図はイメージ図ですが、基本的な地震動予測式による予測値に比べて、平野部では地震動強さが増幅する傾向が見られました。
そこで平野毎の揺れやすさを表現するパラメータとして、堆積層の厚さを加味した補正項を提案しました。「補正あり」の方が平野部の予測精度が向上したことが分かります(※5)
※5:田中裕人・松浦律子・古村美津子・高浜勉, 2023,地震動予測式の残差からみた平野毎の地盤増幅の違い, 日本地震学会秋季大会
動的モード分解による地震観測記録の特徴量分析と工学的解釈
動的モード分解(DMD)について
動的モード分解(DMD; Dynamic Mode Decomposition) とは、時系列データから、主要な時間発展特徴をモードとして取り出すためのデータ駆動型の時系列解析手法の一つです。流体力学分野から発展してきましたが、汎用性や解釈性の高さから、現在では様々な分野での応用が進んでいます。構造計画研究所では、DMDを地震波形の分析や地盤の地震応答解析に応用する試みを進めています。(※6, 7, 8)
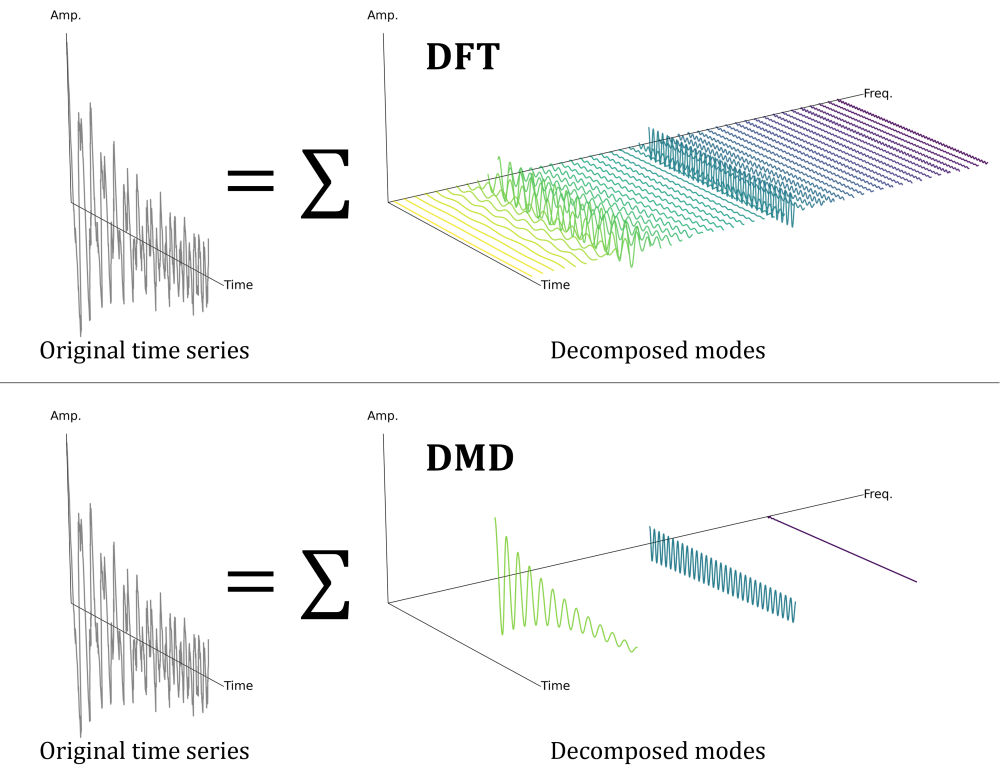
時系列データをモード分解する代表的な手法として離散フーリエ変換(DFT)が挙げられますが、DMDとDFTには以下の違いがあります。
■ DFTの特徴
- 各モードが時間方向に定常な振幅を持ち、固定の周波数間隔に分解される
■ DMDの特徴
- 各モードが固有の周波数と固有の減衰率(または増幅率)を持って分解される
DMDは減衰・増幅を含む力学的に有意な少数のモードによって表現できることから、工学的解釈性の高いモード分解手法と言えます。
DMDの適用事例
DMDを地盤の地震応答解析に利用した取組をご紹介します。
ここでは基礎検討として、地盤の周波数応答解析結果に対してDMDを適用し、地盤特性の特徴量抽出と工学的解釈を試みました。
利用するデータは地表と地中の2点における地震波形のみです。
地盤の地震応答解析に必要な層厚、密度、剛性、減衰などの地盤情報は一切利用せず、加速度の時系列データのみを利用している点に特徴があります。
以下に本検討における実施内容のポイントを示します。
| 対象地盤 |
|
| 解析手法 |
|
| DMDの分析対象データ |
|
| アウトプット |
|
| 検証方法 |
|
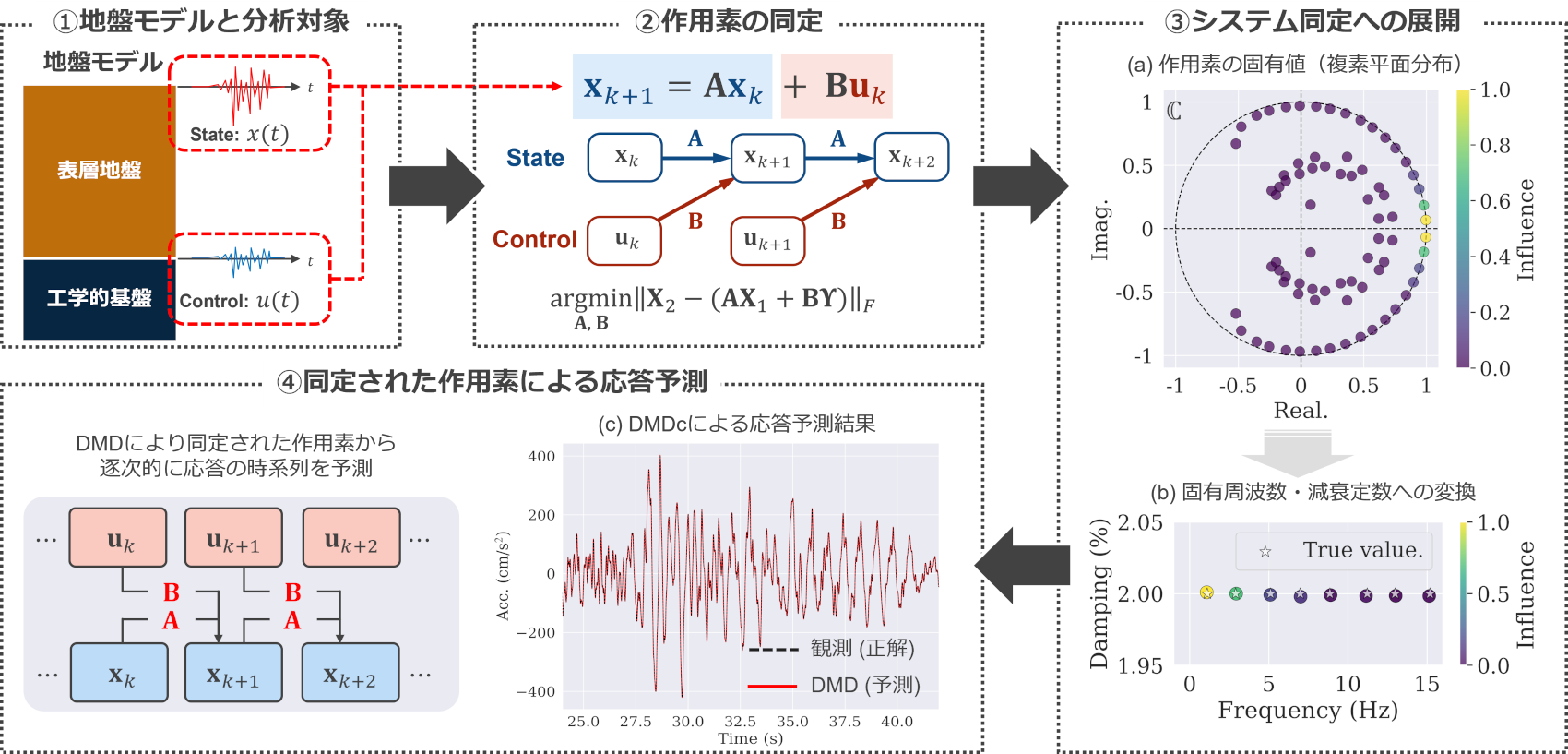
実施した検討のフローおよび結果を下図に示します。
以下、順を追ってご説明します。
①地盤モデルと分析対象
観測地震波を仮想地盤モデルの基盤に入力し、周波数応答解析を実施して地表応答をシミュレーションします。入力地震波(基盤波)と周波数応答解析の出力結果(地表応答波形)にDMDを適用しました。
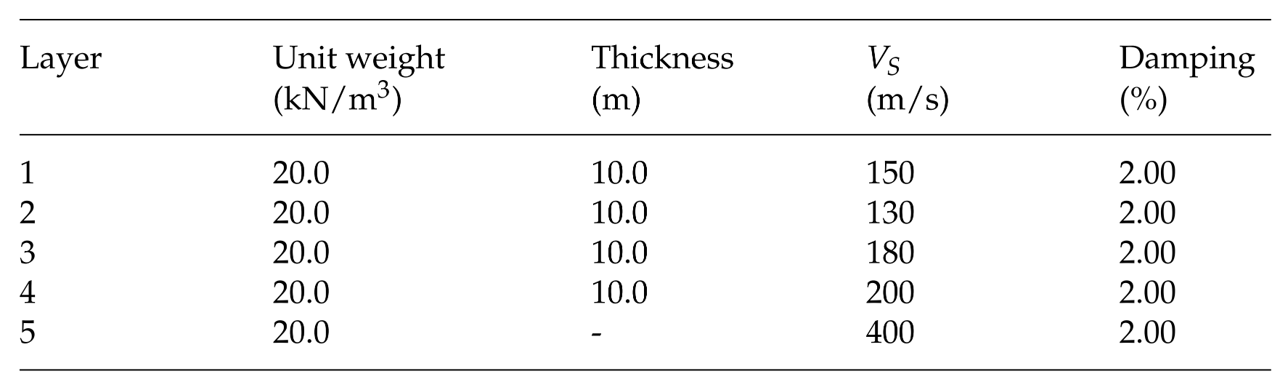
下表に仮想地盤モデルを示します。全層一律で減衰定数を2%としました。
②作用素の同定
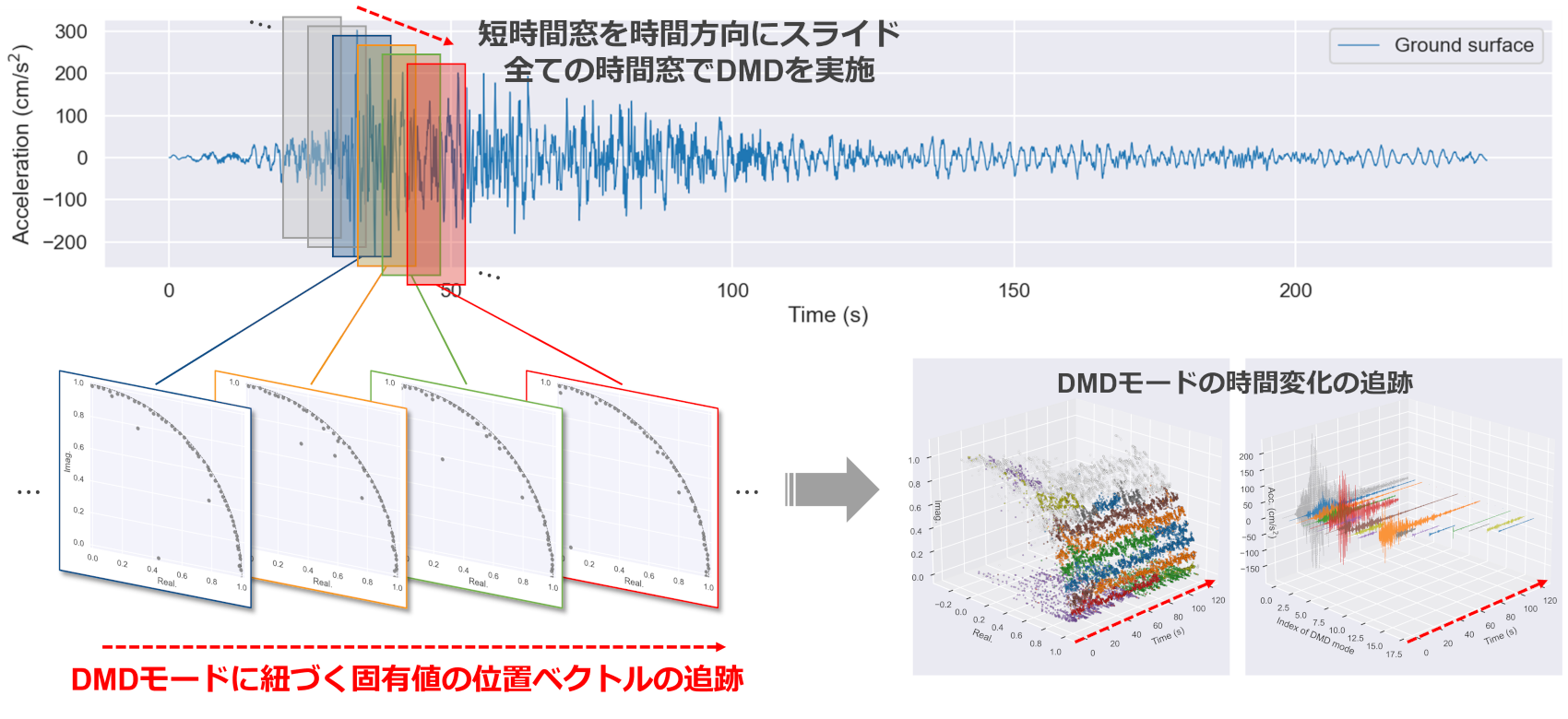
DMDにより地盤応答を「作用素」として抽出します。作用素からDMDモードと各モードの固有減衰定数・固有周波数が求まりますので、得られたDMDモードや作用素の妥当性を検証しました。
③システム同定への拡張
DMDによって得られた作用素の固有値を図中(a)に示しています。これらは固有周波数・固有減衰定数に変換されます(図中(b))。
図中(b)には、別途、地盤モデルの情報が要求される固有値解析によって求めた地盤の固有周波数と仮定した減衰定数2%を☆印で示しています。主要なモード(※)では、DMDによって得られた固有値が、地盤モデルの仮定条件(固有周波数・減衰定数)とほぼ一致していることが確認できます。
※固有値のコンター色はDMDモードの重要度(データ全体への寄与度)を示す。
④同定された作用素による応答予測
図中(c)は、得られた作用素、入力波を用いて、地表応答を予測した結果です。黒色破線は周波数応答解析結果(正解値)、赤色線がDMDによる予測結果であり、両者はほぼ重なっています。振幅や位相の特徴がよく捉えられており、地盤の地震応答の時間発展がDMDの作用素として適切に抽出されていることが確認出来ました。
DMDの可能性
上記の基礎検討により、DMDを地盤の地震応答解析に応用できる可能性が示されました。特に層構成や地盤パラメータを利用せずに、2地点の加速度波形から応答予測や地盤パラメータ推定ができることから、将来的には地盤調査結果の無い場所や地盤のモデル化が困難である広域・多地点に対する地震応答解析の他、引き戻し解析等への活用が期待されます。
今後の重要な課題として、時刻歴非線形解析や強震観測記録など、地盤特性が時間変化する非線形問題への対応があります。
現在は非線形問題への発展を見据え、様々なDMDの拡張手法の検討を進めています。例えば下図の例では、時間方向にスライドする短時間窓区間においてDMDを適用し、作用素の時間変化を追跡することで、非線形現象への適用性を向上させることを試みています。
※6:Akihiro Shioi, Yu Otake, 2024, Time series analysis of seismic ground response via dynamic mode decomposition with time-delay embedding, 4th International Conference on Vulnerability and Risk Analysis and Management (ICVRAM2024) & 8th International Symposium on Uncertainty Modelling and Analysis (ISUMA2024)
※7:塩井瑛大・大竹雄・吉田郁政・村松正吾, 2024, 時間遅延埋め込み動的モード分解に基づくデータ駆動型地震応答解析, 土木学会論文集, 第80巻15号
※8:塩井瑛大・大竹雄・浅野湖太郎・ウィリアムズ=リカー フランシスコ, 2024, 動的モード分解を用いた地震動の状態遷移メカニズム同定に向けた基礎研究:モード追跡による時系列分解, 第27回応用力学シンポジウム
機械学習による応答スペクトル予測
理学分野ではフーリエスペクトルに基づく分析がよく行われますが、工学分野ではPGA(最大加速度)、PGV(最大速度)、応答スペクトル等の指標が多く用いられます。
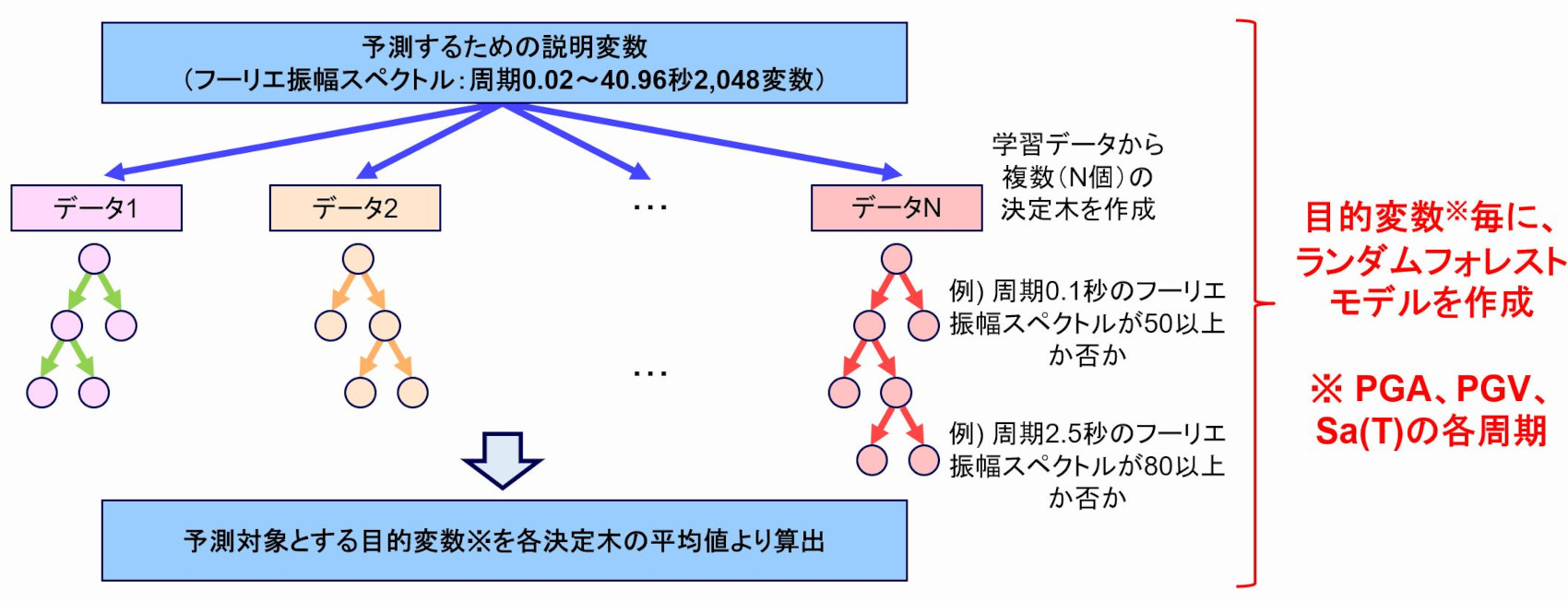
そこで機械学習を用いて、地震観測記録のフーリエ振幅スペクトルからPGA、PGV、及び加速度応答スペクトルを予測する研究を行っています(※9)
防災科学技術研究所のK-NET及びKiK-netで観測された1997年1月から2023年4月までの観測記録を学習し、2023年5月5日に石川県能登地方で発生した本震と最大余震を対象に各指標の予測を試みました。
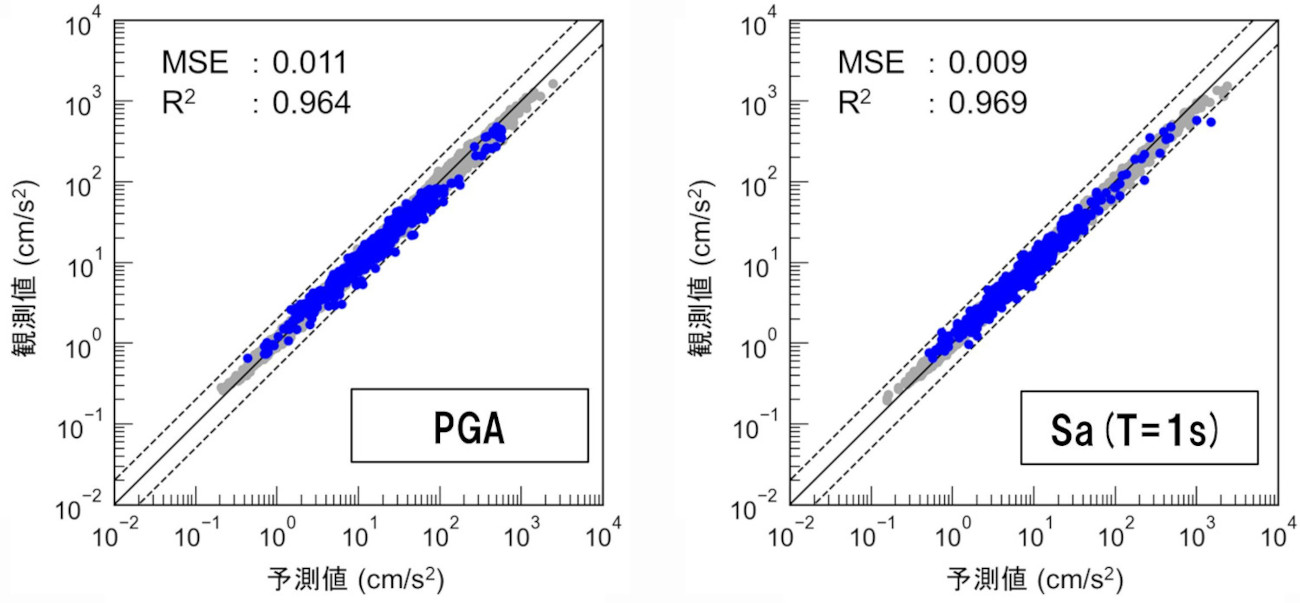
その結果、PGAや加速度応答スペクトル(周期1秒)はある程度精度の良いモデルを構築することができました(特に青色で示す予測値)。
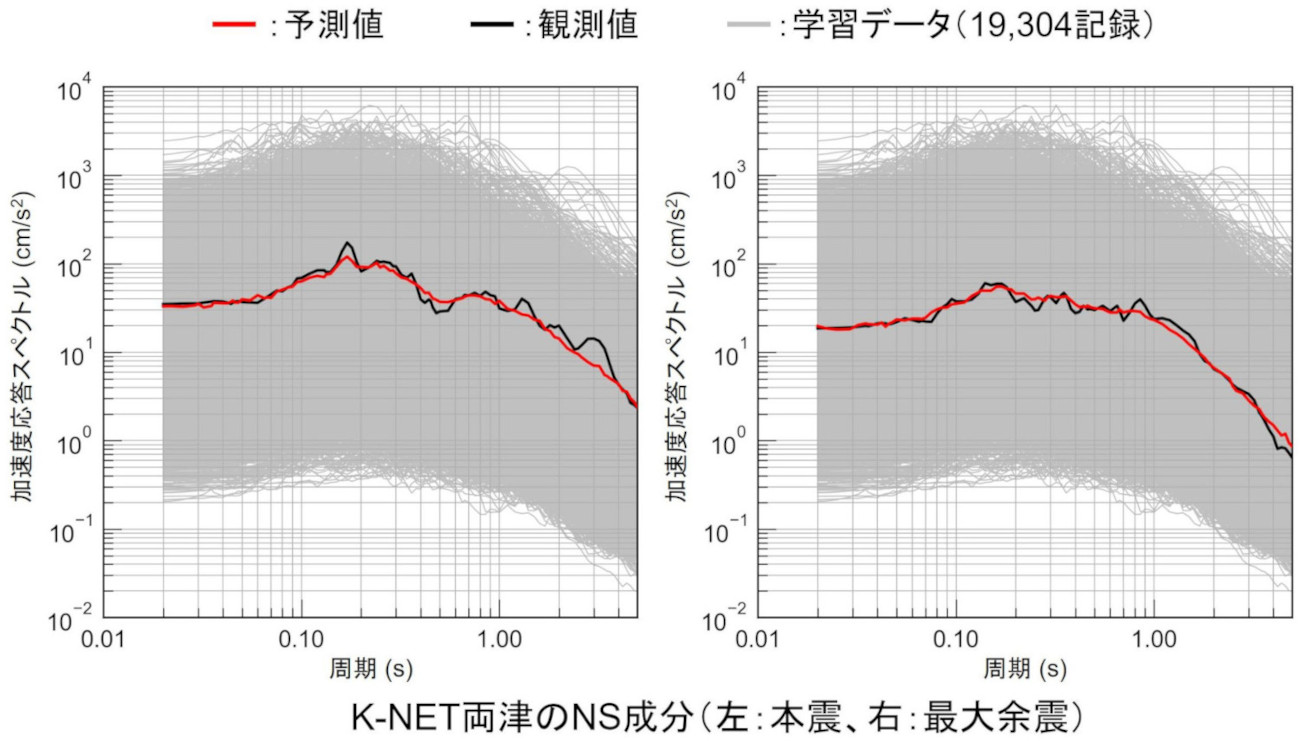
また、下図はK-NET両津地点における加速度応答スペクトルの検証例です。左が本震、右が最大余震です。図中の黒線がターゲットの観測値です。灰色で示した学習データを用いて構築した予測モデルを用いて、フーリエスペクトルから応答スペクトルを予測した結果が赤線です。
学習データの密度が高い応答レベル(中間レベル)という事もあり、概ね精度良く予測が出来ています。
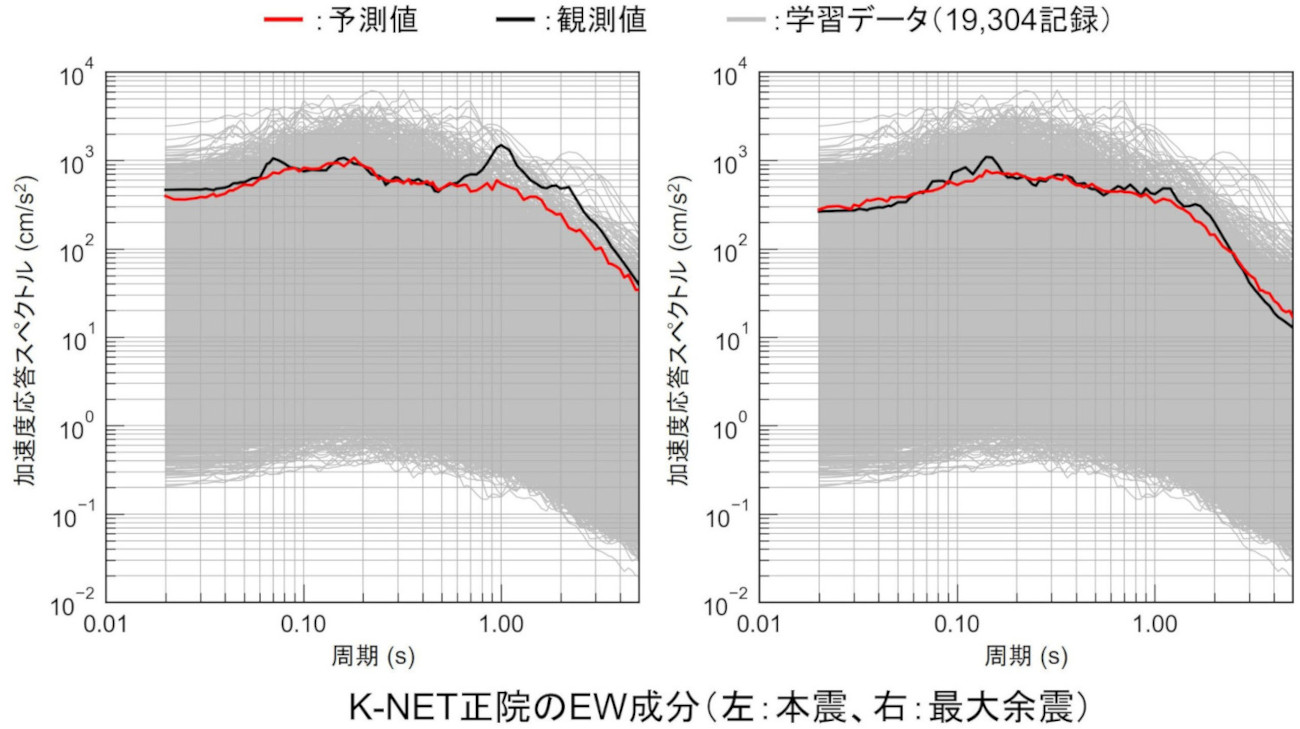
一方、学習データの中では応答レベルが大きいK-NET正院の予測例を下図に示します。
特に左図の本震の周期1~3秒程度において観測値と予測値の乖離が大きくなっています。学習データの密度が低くなる高い応答レベルであることに加えて、観測波形のパルス性の影響で観測スペクトルが大きくなっている事が考えられます。
今後も予測精度の向上のため、より良い説明変数の取り扱いや、より適した機械学習手法の試行を進めてまいります。
※9:倉田悠暉・他, 2023,機械学習によるフーリエ振幅スペクトルから応答スペクトルを予測する試み, 日本地震学会秋季大会
地震動研究支援 資料ダウンロード
構造計画研究所では地震動や地盤、構造物の高度な解析・分析技術を基に、お客様の研究開発支援や事業継続上の課題解決支援(実地震被害の要因分析や対策案の検討、過去の観測記録の分析やDB化など)を行っています。
個別のご紹介・ご相談も承っておりますので、お気軽にお問い合わせください。
「地震動研究支援」ダウンロード資料
「地震動研究支援」の技術資料(PDF形式)を無料でダウンロードいただけます。
設計用入力地震動作成サービスについて
本ページは高い専門性が必要となる個別課題に対する当社のサービス紹介となりますが、別途、お客様の設計実務のご支援として、各種構造物の耐震設計で必要となる地震動を作成するサービスのご紹介も行っています。下記リンクよりご確認ください。
資料ダウンロード
さまざまな解析技術をまとめた資料をダウンロードいただけます。
解析技術の概要から、具体的な事例まで詳しくご紹介しています。ぜひ一度ご覧ください。