AIによる力学系の表現と将来予測
近年の気候変動や社会インフラの複雑化に伴い、様々な物理現象に対する高精度な将来予測の重要性が増しています。予測に用いられる手法は、物理法則に基づくシミュレーションと、観測データに基づく統計・機械学習的な手法(AI)に大別されます。
物理モデルは、対象現象のメカニズムを微分方程式などで表現し、少ないデータからでも一定の予測を可能にする強力な手法です。しかしその一方、現象のモデル化自体が困難であったり、多くの仮定を置く必要があったり、計算時間や数値安定性の問題からリアルタイムに運用できなかったり等の課題があります。
対照的に、AIに代表される機械学習モデルは、特定のモデルを仮定せず、データ間に存在する複雑な関係を巧みに捉えることができます。しかし、高い性能を十分に発揮するには大量の学習データを必要とする点や、学習データに含まれない未知事象(外挿)への対応、予測のブラックボックス化が課題となります。
ここでは、これらの課題に対し、両者の境界領域に位置し、それぞれの利点を融合するアプローチとして注目を集める、力学系理論を応用したデータ駆動型の予測手法を紹介します(図1)。本手法は経験的動的モデリング(Empirical Dynamic Modeling)とも呼ばれます。その原理と応用事例、そして周辺領域の技術と今後の展望を解説します。

図1:経験的動的モデリングの位置づけ
経験的動的モデリングの原理
力学系理論からのアプローチ
経験的動的モデリングは、現象を支配する方程式が不明でも、観測された時系列データには背後の力学系情報が本質的に含まれる、との考えを基礎とします。
一見不規則で複雑な時系列データも、決定論的なシステム(力学系)から生じていれば、振る舞いは「アトラクタ」と呼ばれる幾何学的構造として解釈できます(図2)。アトラクタはいわばシステムの「振る舞いの地図」であり、軌跡を追跡して将来の状態を予測します。
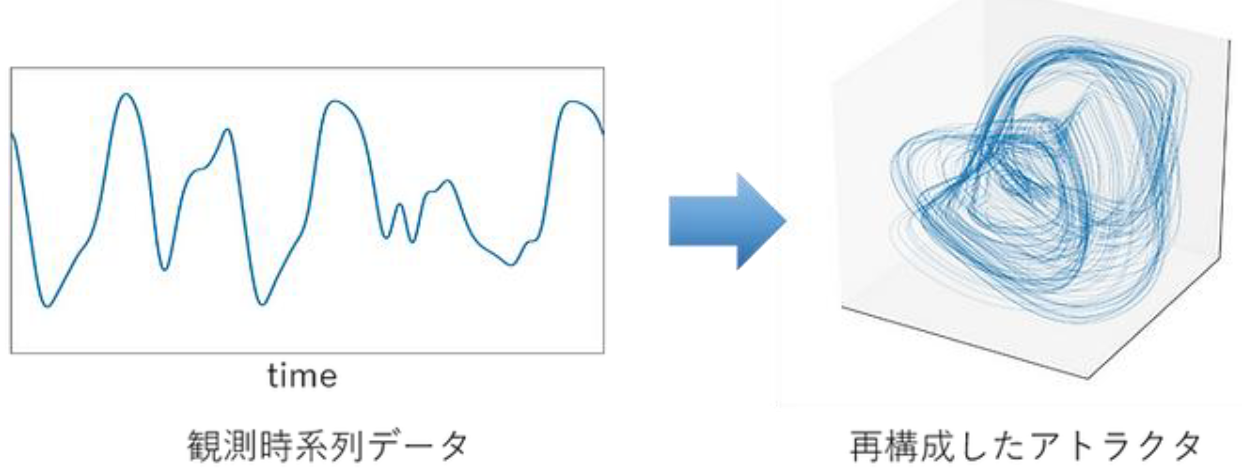
図2:複雑な時系列の背後にある決定論的な構造(アトラクタ)とその変換
本理論の根幹を成すのがTakens’の埋め込み定理 [1] です。本手法では同定理を応用し、システムの一部の変数の時系列データとその遅れ座標を複数組み合わせ、元の多次元システムが持つ力学的特性を保持したまま状態空間を再構成します(図3)。
つまり、一つの観測データから、現象全体のダイナミクスを復元します。再構成されたアトラクタ上で、現在の状態に類似した過去の状態点を見つけ出し、時間発展を未来の予測に利用します。

図3:遅れ座標埋め込みによる状態空間の再構成
手法の特徴
本アプローチには、従来の物理モデルや機械学習モデルと異なった以下の特徴があります。
物理モデルの仮定が不要
観測データから直接、現象の振る舞いをモデル化するため、支配方程式を具体的に定義する必要はない。これにより、モデル化が困難な複雑系にも適用できる。
少数データからの学習
状態空間における近傍点を見つけ出す局所的アプローチのため、必ずしも深層学習のような膨大な学習データを必要とせず、データが限られるケースにも適用できる。
力学特性の保持
元のシステムの幾何学的軌道を再現するため、学習データに含まれない未経験の規模の事象に対しても周辺のヤコビ行列を推定することで一定の外挿性能が期待できる[2, 3]。この特性は、既知データの範囲内での内挿に留まりがちな多くの機械学習モデルと大きく異なる。
因果関係の推定
複数の時系列が与えられた際、一方の時系列のアトラクタから他方の値をどの程度うまく推定できるか相互に検証し、単なる相関関係に留まらず、原因と結果を特定する手法(Convergent Cross Mapping)にも応用できる。
応用事例
洪水予測:リアルタイム洪水予測システム「RiverCast®」
本技術を応用した代表例が、リアルタイム洪水予測システム「RiverCast®」です。これは、東京大学との共同研究成果を応用し、観測雨量や河川水位データから15時間先までの水位変動を高精度に予測するシステムです [2, 3]。
国内の複数河川を対象とした精度検証では、物理モデルの分布型流出モデルや、代表的なAIの深層学習モデルと比較して、より高い予測精度 (低いRMSE:二乗平均平方根誤差)を示しました(図4)。
本成果[2]は学術的にも評価され、Scientific Reportsにおいて、2020年の物理学分野で最もダウンロードされた論文トップ100に選出されています。

図4:予測手法の精度比較
特筆すべきは、一般的なAIが苦手とする学習データにない規模の洪水(過去最大規模のピーク)に対しても、力学系の性質を反映して良好な予測結果を示した点です(図5) [2]。

図5:学習データにない規模の洪水に対する予測性能
高潮予測:沿岸域の防災支援
本予測技術は、高潮予測にも応用されています。
風、気圧、水位の観測データを入力とし、東京湾における高潮を高精度に予測した事例では、気象庁が提供する数値シミュレーションと統計補正を組み合わせた高潮ガイダンスの予測値と比較しても、より誤差の小さい結果が得られました(図6) [4]。
高精度な予測情報は、水門や排水機場など沿岸施設の的確かつ迅速な操作判断の支援に活用され、都民の安全確保に貢献しています。
![図6:高潮予測における精度比較 [4]](/images/consulting/flood/page15/img-1-6.svg)
図6:高潮予測における精度比較 [4]
ダム流入量・風速予測: 水資源管理とエネルギー分野への展開
本技術の適用範囲は洪水や高潮に留まりません。ダム流域の雨量や上流水位データからダムへの流入量を予測し、治水効果の最大化や利水(発電量向上)運用の最適化に貢献します。
過去の学習データ最大値を上回る規模の流入量に対しても、変動パターンを捉え、良好な予測を実現します(図7)。

図7:過去データを上回る規模のダム流入量予測事例
さらに、再生可能エネルギー分野でも応用が進んでいます。
風力発電量予測への応用を見据えた風速予測の事例では、気象予報の補正値や代表的なAI手法よりも高い精度で局所的な風速を予測できる可能性を示し(図8)、エネルギーの安定供給に資する技術としての展開が期待されています。

図8:風速予測における精度比較
予測の「不確実性」の定量化と意思決定への活用
予測は常に何らかの誤差を伴い、特に予測の入力となる気象予報の不確実性は、河川水位や流入量の予測結果に大きな影響を与える共通の課題です(図9) [5]。

図9:予報雨量の誤差と確率分布でのモデル化
そこで本アプローチでは、予測値を一点で示すだけでなく、気象予報やモデル自体の誤差を考慮した予測の「幅(信頼区間)」や、利用者が設定した基準値(例えば、避難判断水位や作業中止水位)を超過する「確率」を定量的に算出できます(図10)。
確率的なアプローチにより、予測の信頼度を客観的に評価することができます。

図10:予測の不確実性を考慮した確率的な予測情報の提示例
確率的な予測情報は、防災や事業継続における意思決定の質を大きく向上させます。
たとえば現場のオペレーションにおいて、「対策を講じたが空振りに終わるコスト(機会損失)」と「対応の遅れ(見逃しリスク)による被害コスト」は常にトレードオフの関係にあります。
確率情報を活用すれば、リスクバランスを定量的に評価し、各組織の許容リスクに応じた客観的で合理的な判断基準を予め策定することができます(図11)。

図11:見逃し率と空振り率のトレードオフ関係と最適な判断基準の考え方
力学を考慮したAIの展開
ここで紹介した経験的動的モデリングは、力学を考慮したAIのアプローチの一つですが、本分野の研究開発はさらに広がりを見せています。
たとえば、Reservoir ComputingやNeural Operatorなどの手法も、同様に力学系の性質を利用した予測技術として注目されており、構造計画研究所でも技術開発と応用を進めています。
Reservoir Computingは、ランダムに結合されたニューラルネットワークを用いて入力信号を一旦高次元空間に写し、応答から出力を学習し力学系を再現する枠組みです。学習が高速かつハイパーパラメータも少なく、本特性を活かして多数の拠点を一括で水位予測する仕組みを提供しています(図12)。

図12:Next Generation Reservoir Computerの概念図と多地点水位予測への応用例
一連の動向は、Scientific Machine Learning (SciML) の潮流の一部と捉えることができます。SciMLにはPhysics-Informed Neural Networks (PINN)やPhysics-Informed Neural Operator (PINO)[6]などがあります。
これらは、観測データに加え、物理法則などの科学的知見を明示的に機械学習モデルに組み込み、データの少ない問題や物理的整合性が重要な問題に対し、より信頼性の高い予測を目指す研究分野であり、構造計画研究所では本技術を応用した浸水計算に取り組んでいます。
おわりに
ここで紹介した経験的動的モデリングは、観測データから直接、対象現象の力学的な振る舞いを捉え、従来の物理モデルと統計・機械学習モデルの間のギャップを埋めるデータ駆動型のアプローチです。
予測精度のみならず、不確実性を定量化して合理的な意思決定を支援する枠組みが、応用可能性をさらに広げています。
経験的動的モデリングをはじめとするこれらのアプローチは、「シミュレーションモデルの構築が困難」「学習データが限定的」「メカニズムの理解が重要」などの特性を持つ課題に対し、有効な選択肢を提供します。
構造計画研究所では、PoC(概念実証)からシステム化、さらには予測情報を活用した運用コンサルティングまで、一気通貫で課題解決を支援するソリューションを提供しています。
参考文献
- [1] Takens, F. (1981). Detecting strange attractors in turbulence. In: D. Rand, L.S. Young (eds) Dynamical Systems and Turbulence, Warwick 1980. Lecture Notes in Mathematics, vol 898. Springer, Berlin, Heidelberg.
- [2] Okuno, S., Ikeuchi, K., & Aihara, K. (2020). Practical data-driven flood forecasting based on dynamical systems theory. Scientific Reports, 10(1), 664.
- [3] Okuno, S., Aihara, K., & Hirata, Y. (2021). Forecasting high-dimensional dynamics exploiting suboptimal embeddings. Water Resources Research, 57(3), e2020WR028427.
- [4] 瀧川宏樹, 奥野峻也, (2024). 力学系理論に基づく高潮・高波のアンサンブル予測手法の提案. 土木学会論文集B3(海洋開発), 80(1), 24-17037.
- [5] 奥野峻也, 瀧川宏樹, 宮藤秀之, (2020). 降雨の時空間的な誤差構造を考慮したアンサンブル流出予測. 河川技術論文集, 26, 323-328.
- [6] Li, Z., Zheng, H., Kovachki, N., Jin, D., Chen, H., Liu, B., Azizzadenesheli, K., & Anandkumar, A. (2024). Physics-Informed Neural Operator for Learning Partial Differential Equations. ACM/IMS Journal of Data Science, 1(3), Article 9.
参考:RiverCastご利用実績(敬称略)
公的機関:
国土交通省 徳島河川国道事務所、山形県鶴岡市、神奈川県川崎市、熊本県大津町、福島県福島市、静岡県藤枝市、また実証試験として大阪府、神奈川県横浜市、神奈川県川崎市、ほか全国13自治体45地点以上でご利用。
民間企業:
鹿島建設、清水建設、大林組、西松建設、西武建設、前田建設工業、大本組、横河NSエンジニアリング、ほか建設業、遊水池管理施設、インフラ事業者など多数。
資料ダウンロード
RiverCastパンフレットやセミナー資料等がダウンロードできます。
リアルタイム洪水予測システム「RiverCast」紹介資料関連ページ
解析技術事例集ダウンロード
さまざまな解析技術をまとめた資料をダウンロードいただけます。
解析技術の概要から、具体的な事例まで詳しくご紹介しています。ぜひ一度ご覧ください。
