周波数応答解析の基礎

はじめに

　私たちの日常⽣活で⼀般的に発⽣する物理現象のほとんどは時間に応じる変化の動的挙動ですが、 「音」や「光」などは 〇〇Hzなどで表現されることが多く、 “周波数”は意外に身近なものです。

　物体の動的挙動を解析する⽅法は、 変動を 「時間によって観察するか 《時間領域》 」または「周波数に基づいて観察するか 《周波数領域》 」の⼤きく２つに区分することができます。

　今回は、 周波数に基づいて観察する「周波数応答解析」の基礎について記載します。

周波数応答解析とは？

　周波数応答解析とは、 物体の挙動を時間領域から周波数領域に変換し、周波数ごとに動的応答を分析する⼿法です。

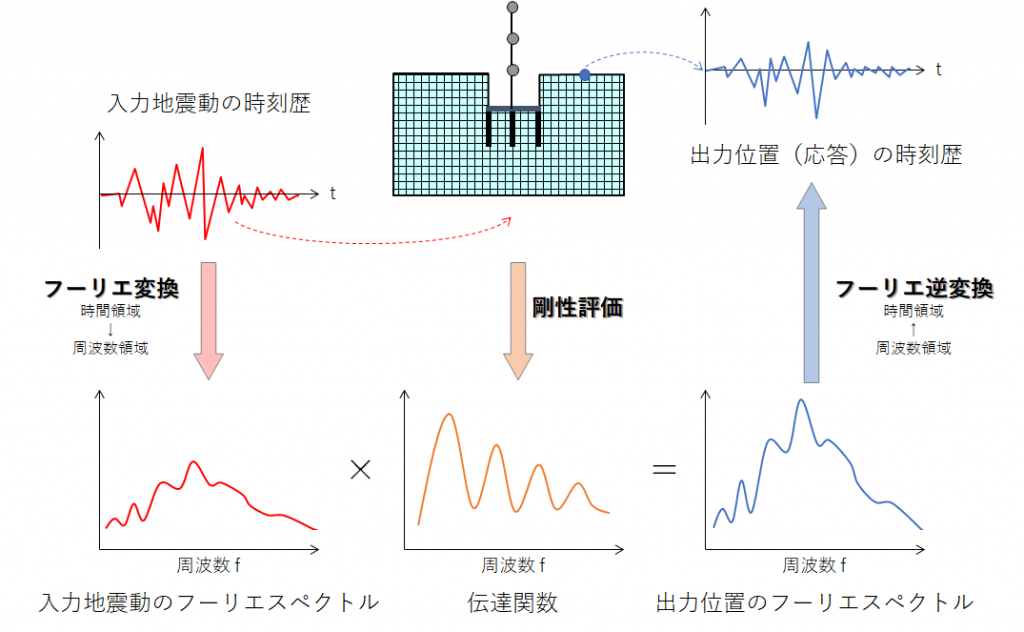
解析手順の概要は以下の通りです。

（1）入力地震動の時刻歴波形をフーリエ変換により時間領域から
周波数領域に変換し、入力地震動のフーリエスペクトルを算出する

（2）解析モデルの剛性評価から応答算出節点の伝達関数を算出する

（3）入力地震動のフーリエスペクトル に伝達関数を掛けて、
応答算出節点のフーリエスペクトルを算出する

（4）応答算出節点のフーリエスペクトル をフーリエ逆変換により
周波数領域 から時間領域に変換し、 節点応答の時刻歴波形を算出する。

フーリエ変換とは？

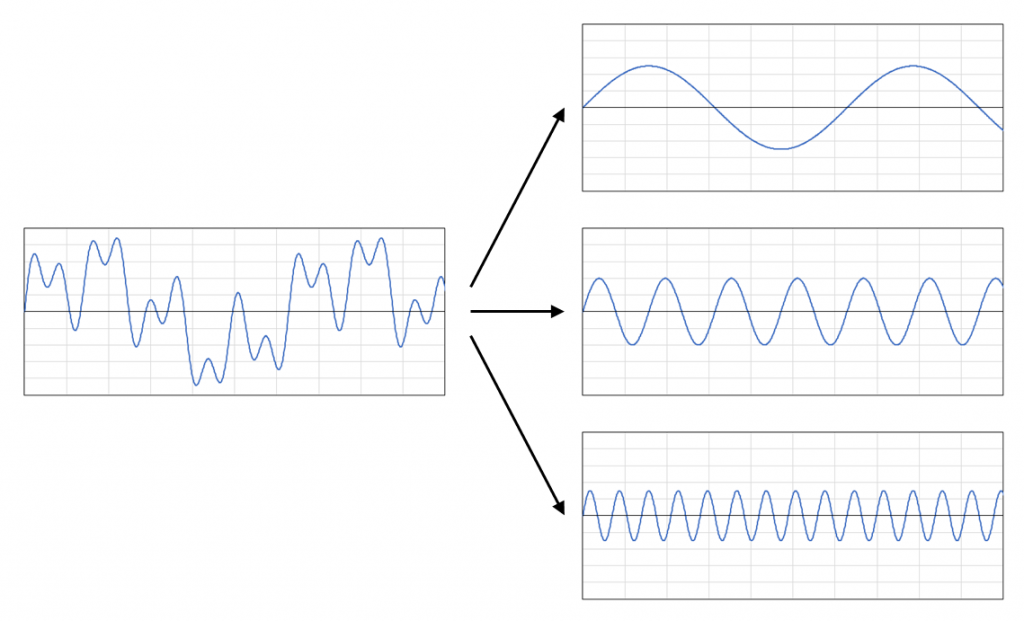
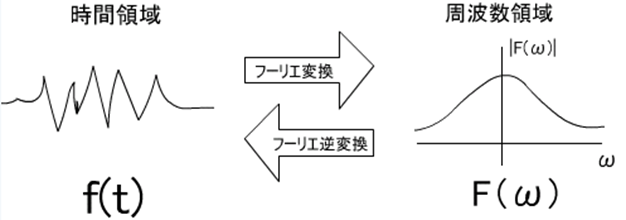
　フーリエ変換をざっくりいうと「 ある波形を正弦波のような性質の良くわかっている波形の重ねあわせで表現する 」といった感じです。例えば下図の左側の複雑な波形も 周波数ごとに振幅が異なる 正弦波（振動）の重ね合わせで表現することができます 。

フーリエ級数

任意の周期関数f(t)は、 三角関数（sin , cos）の和で表現できる。

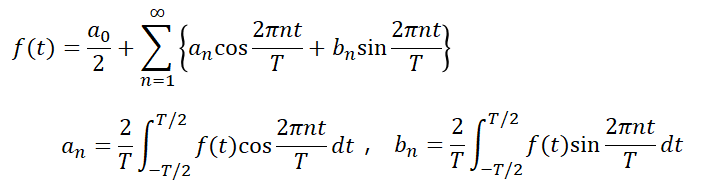
複素フーリエ級数

フーリエ級数では、sin と cos に分かれているので、オイラーの公式を使用すると三角関数は以下のように表現できる。

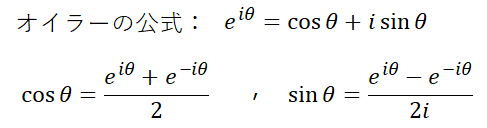
上式をフーリエ級数に代入する。

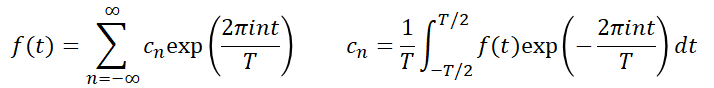
フーリエ変換/逆変換

複素フーリエ級数について、とおくと、

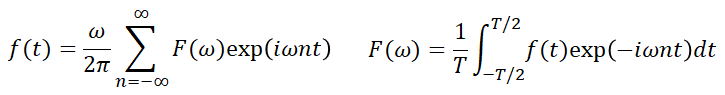
ここで、T→∞を考えると、複素フーリエ級数は次のようになる

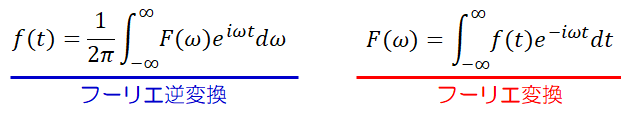
伝達関数

　周波数ごとに単位振幅の入力地震動に対する応答を表しており“増幅率”とも呼ばれ、構造物の特性、地盤の種類や 地形等により異なります。

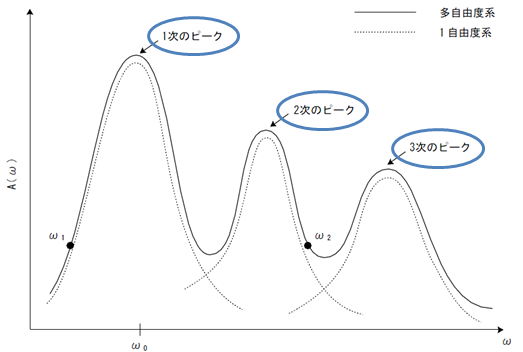
（参考）基礎方程式

まとめ

今回は 「周波数応答解析」の基礎について 説明しました。