はじめに
人工知能(AI)、それは時代の最も魅力的な言葉であり、分野横断的にその応用は飛躍的に拡大しています。携帯電話の音声認識ソフトや車のナビなど、私たちの身の回りのあらゆるところにAIが存在しています。Googleも検索エンジンにAIを利用しています。Netflixやamazonプライムの映画提案は、AIがベースになっています。SiriやAlexa、Googleアシスタントとの対話も、AIの一種です。
AIとは何か?
1940〜1950年代に登場して以来、さまざまな用語や定義で呼ばれてきましたが、簡単に言えば、AIはコンピュータサイエンスの一分野であり、従来は人間の知性を必要としたことをコンピュータで行うことです。
AIは半世紀以上前から存在していましたが、データ量の増加、アルゴリズムの進化、コンピューティングパワー&ストレージの向上により、最近になって様々な産業で応用されるようになりました。
AIによる構造ヘルスモニタリング
構造工学分野でのAIの応用としては、構造ヘルスモニタリング(SHM)が最も多く見られます。センサーなどのデータ取得システムの進歩により、構造物の正確な診断に必要なデータを取得することが可能になりました。一方、AIはデータのパターンを学習し、与えられた入力に対する出力を予測する能力を備えています。以上のような年表を見ると、データ収集システムで取得したデータをAI技術で学習し、構造物の安全性を判断してはどうか、と考えたくなります。
そこで、構造計画研究所のRESPチームは、社内で検討を行い、建物の損傷有無を判断できるモデルを開発しました。本記事では、その概要を簡単に紹介します。
背景説明
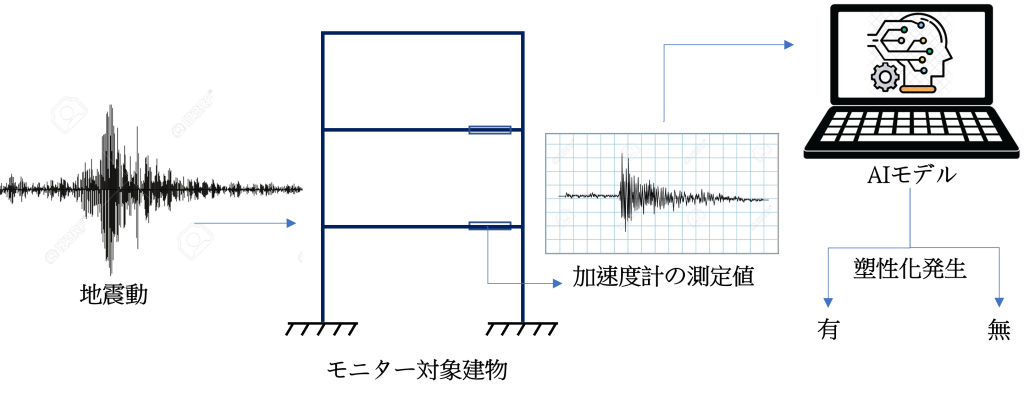
通常のシステムでは、建物や地表に設置した加速度計の測定値から、既存構造物の応答(層間変位、層間変形角など)を算出します。
しかし、本検討では、応答加速度時刻歴から直接建物の損傷有無を予備的に判断できるAIモデルの開発に焦点を当てました。これにより、加速度計から取得したデータの処理に要する時間を短縮することができます。また、地表に加速度計を設置する必要がなくなります。提案システムの概要を下図に示します。
機械学習における時系列データの扱い方
構造物の応答加速度時刻歴は時系列データです。時系列の問題に対する標準的なアプローチでは、通常、機械学習アルゴリズムに入力できる特徴を手動で抽出する必要があります。特徴抽出には、一般的にデータの元となる分野の知識が必要とされます。
画像分類のように、分類アルゴリズムで使用できる画像データの特徴を手動で抽出する必要がありましたが、深層学習(ディープラーニング)の出現により、特徴抽出はモデル自体から行えるようになりました。つまり、深層学習のモデルは、自ら多くのフィルターを通して特徴を抽出します。
本検討では、畳み込みニューラルネットワーク(画像分類で広く使われている深層学習モデル)を用いて時系列データ(応答加速度時刻歴データ)を分類することで、建物損傷の有無の予測を行いました。
データ記述
まずはシンプルなモデルを仮定することとして、完全弾塑性バイリニア一質点系モデルを検討しました。固有周期1.0sと1.2sのモデルをElCentro NS、Kobe NS、Taft EW、Hachinohe NS、JMA KOBE、とBC J L2の地震動に対して非線形解析を行い、応答加速度時刻歴を出力しました。
塑性率が1を下回る倍率(地震動の入力倍率)から2を超える倍率まで徐々に増加させ、各モデルで合計796の解析ケースを作成しました。
従って、今回のデータセットは、796+796=1592サンプルの応答加速度時刻歴データからなり、各サンプルは塑性化が発生している場合は「1」、発生していない場合は「0」とラベル付けされています。このデータセットは、1列目にラベル、他の列目に時刻歴データで、TSVファイルにまとめられています。
※なお、ここでのデータは、実際の加速度センサーの観測値ではなく、シミュレーションモデル(完全弾塑性バイリニア一質点系モデル)の解析結果に相当するものです。したがって、現実の応用となると、上記とそれに付随する要因(ノイズ等)を考慮する必要があります。
データ処理
機械学習や深層学習では、一般に、まずデータを機械・深層学習アルゴリズムに投入できる形式に加工することが必要です。
データ処理として、現在のデータセットをトレーニングデータとテストデータにそれぞれ66%と33%の割合で分割しました。また、アンバランスデータ(一方のクラスのサンプル数が他方より大幅に多い)であるため、トレーニングデータとテストデータで相対的なクラス頻度がほぼ維持されるようにデータを層化抽出しました。


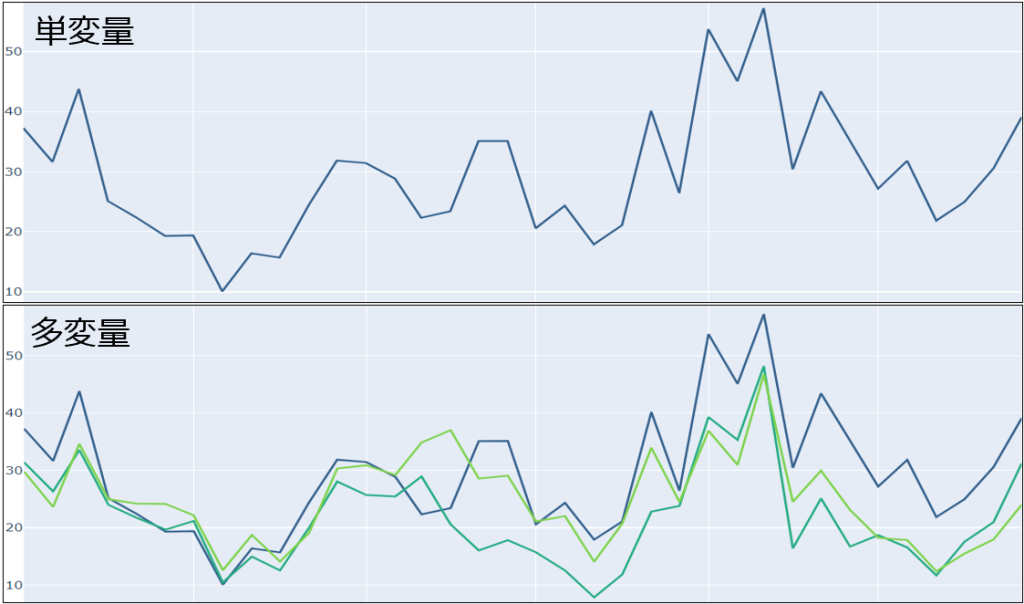
なお、ここで使用した時系列データは単変量であり、時系列例ごとに1つのチャンネルしかないです。しかし、実際には、時系列データは多変量であることがあります(例えば、X、Y、Z方向の加速度時刻歴データ)。そこで、numpy(pythonパッケージ)を用いて、簡単な整形を行うことで、現在のデータを多変量データに適応可能な形式に変換しました。これにより、多変量時系列データに適用しやすいモデルを構築することができます。下図は、単変量と多変量の時系列データの違いをよく表しています。
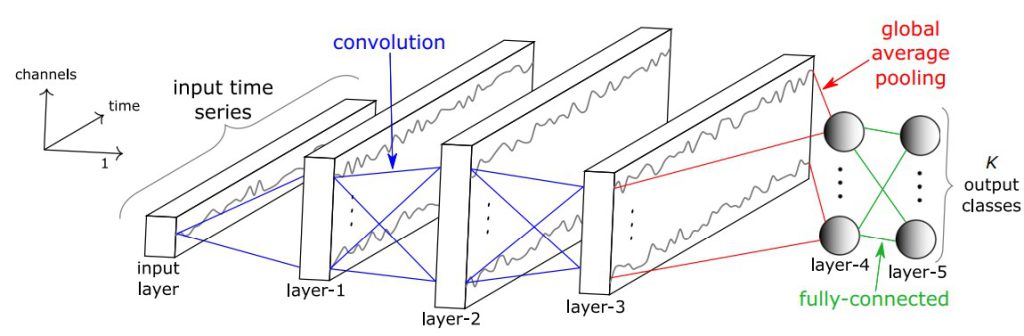
畳み込みニューラルネットワーク(Convolutional Neural Network)
参考文献で提案されているモデルを改良し、畳み込みニューラルネットワーク(アーキテクチャ)を構築しました。そのモデルの模式図を下図に示します。
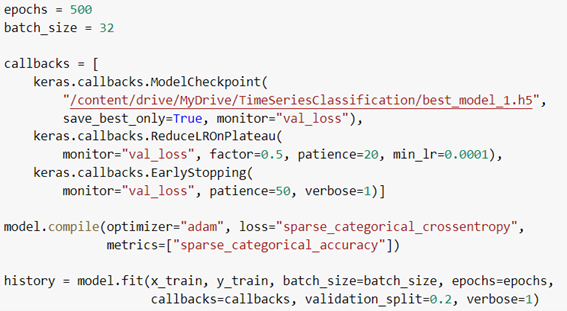
モデル学習
以下の設定で、トレーニングが実行されました。
学習パラメータは下表のようにまとめます。
| 最適化方法 | Adam最適化 | 1次および2次モーメントの適応的な推定に基づく確率的勾配降下法 |
| 初期学習率 | 0.001 | -- |
| 損失関数 | Cross entropy | モデルが学習データセット全体を通過する1サイクル |
| バリデーション分割比率 | 0.2 | バリデーションデータとして使われるトレーニングデータの割合 |
以下のグラフは、各エポックでの学習時に出力されるモデルの損失関数の値と正解率を示したものです。
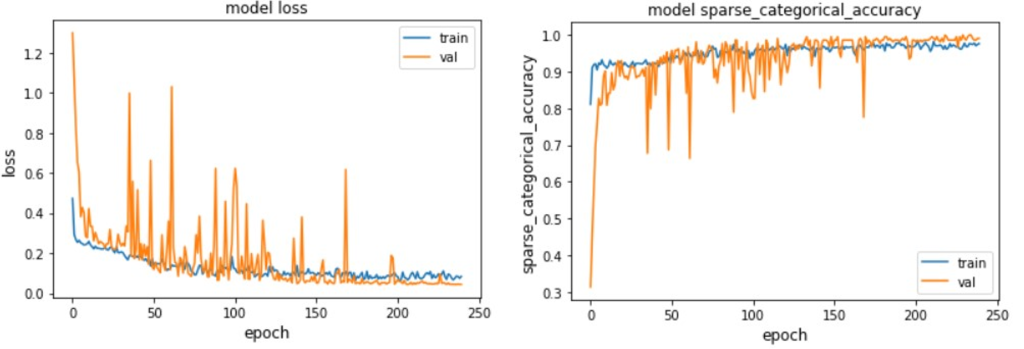
左のグラフは「損失関数値のグラフ」、右のグラフは「正解率のグラフ」です。青線は学習データに対する損失値と正解率、オレンジ線はバリデーションデータに対する損失値と正解率を表します。
ニューラルネットワークの学習では損失関数の値を小さくするように学習が進んでいくため、一般には損失値が小さいほど良いモデルであると考えられます。同様に、正解率が高いほど良い状態となります。グラフから、240回目のエポックでは損失関数が0.2以下に減少し、正解率も95%以上に向上していることが確認できます。これは、学習がしっかりと達成されていることを示しています。
また、バリデーションデータに対する損失値や正解率を、学習データに対する損失値や正解率と一致しているので、オーバーフィット(過学習)は生じていないことがわかります。
※過学習:学習データに対しては良い性能を示すが、バリデーション・テストデータに対しては悪い性能を示す現象
モデル評価
学習したモデルを再ロードし、テストデータに対して評価しました。なお、テストデータは評価用に保存したオリジナルデータの33%です。

正解率を評価基準としてテストデータで評価したモデルは、ほぼ97%の正解率を示しています。しかし、扱う問題やデータセット(バランス、アンバランス)によっては、他の指標(適合率、再現率など)を用いてモデルを評価する必要があります。
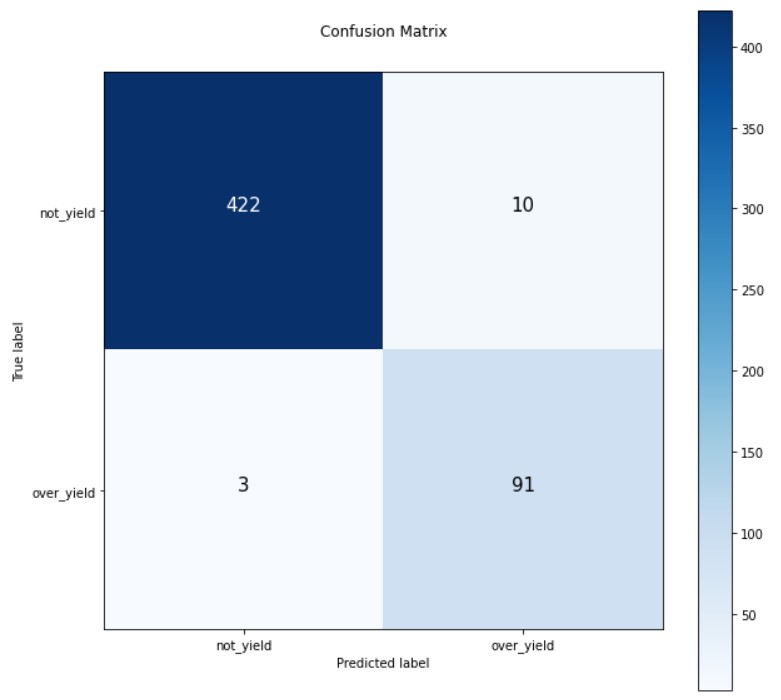
そのため、他の指標に対してモデルを評価するために、confusion_matrixをプロットしました。'not_yield'は「塑性化していない」クラスで、'over_yield'は「塑性化している」クラスです。 'True labels' はサンプルの実際のクラスを表し、'Predicted Labels' は機械学習モデルで予測されたクラスを表します。そういう意味では 、422という数字は、実際に「not_yield」クラスに属し、機械学習モデルによって「not_yield」と予測されたサンプルの数です。一方、10という数字は、実際には「not_yield」クラスに属しているが、モデルによって「over_yield」クラスと予測されたサンプルの数を意味します。
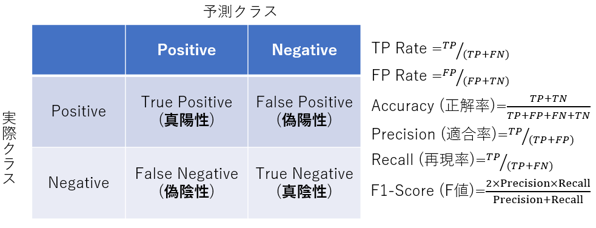
ConfusionMatrixから各種評価指標のスコアを求める方法を下図に示します。
※Confusion Matrixの 「Positive 」と 「Negative 」は、考慮するクラスによって異なります。「over_yield 」クラスを考える場合、「Positive 」は 「over_yield」、「Negative 」は 「not_yield 」を指します。
このようにして得られた評価指標スコアを下表にまとめます。
| ラベル | 適合率 (Precision) | 再現率 (Recall) | F1値 (F1 Score) |
| not_yield | 0.99 | 0.98 | 0.98 |
| over_yield | 0.90 | 0.97 | 0.93 |
| 平均(Average) | 0.95 | 0.97 | 0.96 |
他の評価指標に対して評価した場合、テストデータでのモデルの性能は95%以上であることがわかります。
モデルの適用範囲
前述したように、学習に用いるデータは、固有周期1.0sと1.2sの質点系モデルの時刻歴データです。しかし、実際には、シミュレーションモデルと実際の構造物の固有周期は、一定の幅をもってばらつく場合があります。
したがって、固有周期1.0sと1.2sの質点系モデルの応答時刻歴データで学習させたCNNモデルは、1.0s、1.2sに対してある程度変動した固有周期のモデルデータでもテストする必要があるはずです。そこで、同様に、固有周期0.5s、0.6s、0.7s、0.8s、0.9s、1.1s、1.3s、1.4s、1.5sのモデルの応答加速度時刻歴(同様にラベルを付けた)データからなるTSVファイルを作成することにしました。そして、このデータに対してCNNモデルをテストしました。
下の表は、すべての評価指標に対するモデルの性能値を示しています。
なお、これらの値は、「over_yield」クラス、すなわち「over_yield」クラスが正のクラスとみなされる時に対応することです。
| 固有周期 | 正解率 (Accuracy) | 適合率 (Precision) | 再現率 (Recall) | F1値 (F1 Score) |
| 0.9s、1.1s、1.3s | 0.98 | 0.99 | 0.99 | 0.99 |
| 0.8s、1.4s | 0.98 | 0.98 | 1.00 | 0.99 |
| 0.7s、1.5s | 0.98 | 0.99 | 0.99 | 0.99 |
| 0.5s、0.6s | 0.86 | 0.79 | 1.00 | 0.88 |
評価の結果、固有周期0.7s、0.8s、0.9s、1.1s、1.3s、1.5sのデータに対して、学習済みCNNモデルは良好(90%以上)な性能を発揮することがわかりました。しかし、固有周期0.5sと0.6sのデータにたいしては、性能が悪化しています。
以上の検討から、実際の構造物の固有周期がシミュレーションモデルと最大1.25倍異なる場合でも、精度を保つことができたと判断できます。
まとめ
- 直接建物の応答加速度時刻歴データから損傷有無(塑性化発生)を判断できるAIモデルを開発し、その適用性を評価しました。
- このAIモデルは、学習に用いたモデルデータの固有周期の約1.25倍までの固有周期に対応するデータに対して、良好な性能を示しました。
- なお、本モデルはプロトタイプとして実装したものであり実運用には課題もあると思いますが、プロトタイプとしてはいい精度が出ています。
さいごに
機械学習技術の展開や実装の仕方を見ていると、これからの時代でAIがより活用されることは間違いないでしょう。AIと機械学習技術が第5次産業革命を推進すると多くの人が考えています。そう考えると、今こそ、それぞれの分野でAIの可能性を追求し、ステップアップする良い時期なのではないでしょうか。今回は、構造ヘルスモニタリング領域でのAI活用を例示しましたが、同じようなアイディアの実現にお困りの方はぜひご相談ください。


 (3 投票, 平均: 1.00 / 1)
(3 投票, 平均: 1.00 / 1)