2016年8月4日、土木学会の橋梁の対津波設計に関する研究小委員会により「対津波設計のベンチマークテストに関するシンポジウム」が開催された。構造物に対する津波作用については、各機関で実験や数値解析がさかんに実施されているものの、特に橋梁については未だ対津波設計手法は確立されていない。そこで橋梁に作用する津波波力の各種数値計算手法の特徴や、推定精度を向上させるための工夫・注意点等の知識の共有を目的として、本シンポジウムが開催された。
シンポジウムでは2件のベンチマークテスト課題が事前に公表され、参加者は期日までに計算を実施し、結果を持ち寄る。いずれの課題も津波に関する模型実験を数値計算により再現するものだが、課題1は結果が公開済み、課題2は当日まで結果が非公開のブラインドテストである。弊社では課題1に対してVOF法、課題2に対しては粒子法・VOF法の2つの手法で数値計算を実施し、計3件の発表を行った。 本記事では課題1に対する弊社の数値計算結果を紹介する。
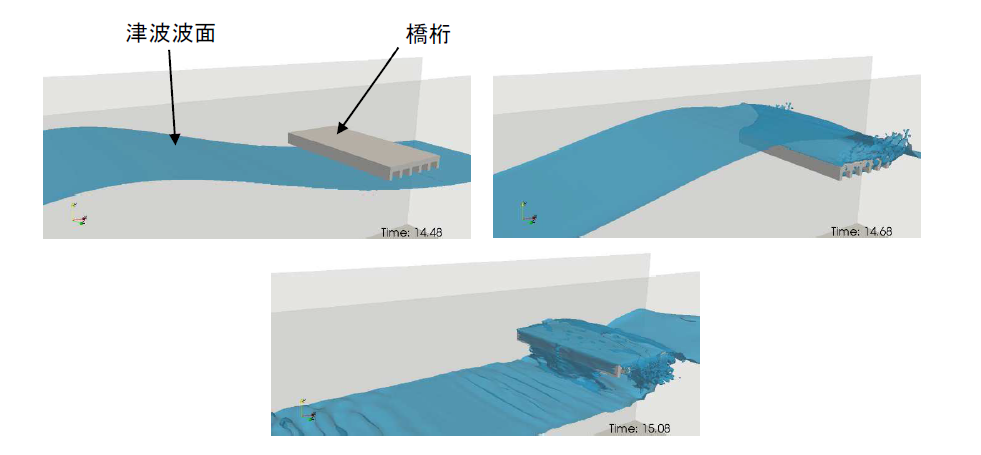
課題 1 は孤立波による橋桁への作用力(抗力および揚力)を求める問題である。実験では水路中央に橋桁模型を設置し、津波を模擬した孤立波を造波させ、模型に作用する津波波力を計測している。1)2)
1.手法
水および空気を非圧縮性粘性流体と仮定し、気液二相流の数値流体解析により橋桁に作用する外力を推定した。解析コードは数値流体力学ツールボックスOpenFOAM4)の標準ソルバの一つinterFoamを用いた。空間の離散化には有限体積法、気液界面の捕捉にはVOF(Volume of Fluid)法、圧力-速度連成手法にはPIMPLE法、乱流モデルとしてSST\(k\) - \( ω\)を適用した。
2.条件
図 1に計算モデルを示す。実験での水位計H2の設置位置から流れ方向へ9.875mの範囲を対象として二次元でモデル化を行い、非構造格子でメッシュ分割を行った。橋桁近傍での格子幅は0.0015m程度であり、モデル全体の格子数は111,596である。解析再現時間はt=9.8~16.0の6.2秒間とした。橋桁および水路底面はノンスリップ条件とし、津波の流出部では速度に関する勾配0条件を与えた。津波の流入部は造波境界とし、実験で得られた水位計H2の波形\(η\)にもとづく液相体積率\(α\)の分布と、水位波形から推定した流速を固定値として与えた。水平方向流速は浅水域における保存波の断面平均流速の算出式 5)により、
\(ū=c \frac {η}{h+η} \)
として鉛直方向に一様の分布を与えた。hは水深、cは波速であり、孤立波理論に基づき波高\(H\)から\(c=\sqrt{g(h+H)}\)とした。鉛直方向流速に関しては次式で自由表面での鉛直方向流速を算出し、\((v)_{y=-h}=0\)となるよう鉛直方向に線形に分布を与えた。
\((v)_{y=η} =\frac{∂η}{∂t}+ ū\frac{∂η}{∂x}\)
また上に述べた造波方法①の他に、造波境界で\(v\)を0固定とした方法②、\(α\)を勾配0とした方法③、\(v\)を0固定かつ\(α\)を勾配0とした方法④の4通りで波高検定を実施し、造波手法を比較した。図 2に結果を示す。①、②、③は実験と良い一致が見られるが、④は実験水位を有意に下回る結果となった。
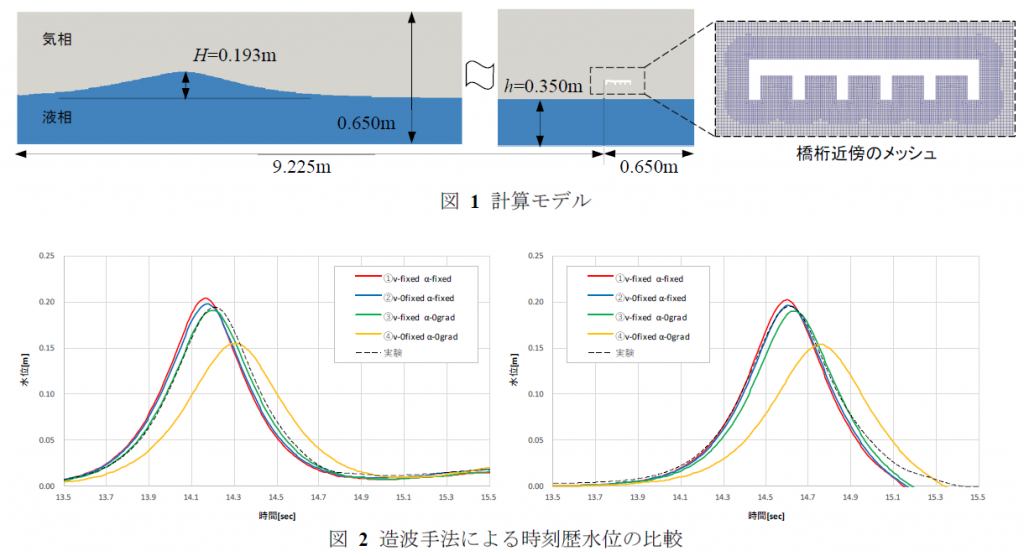
以上の結果より、\(α\)に勾配0条件を与える場合はvを推定して与える必要があり、また\(v\)を推定して与えた場合は\(α\)について勾配0としても造波が可能であると言える。ただし図 3に示す通り、方法②~③は造波直後に波面の乱れが見られるのに対し、方法①は造波直後から波面を安定して再現できたため、本計算では方法①による造波手法を採用した。

3.結果
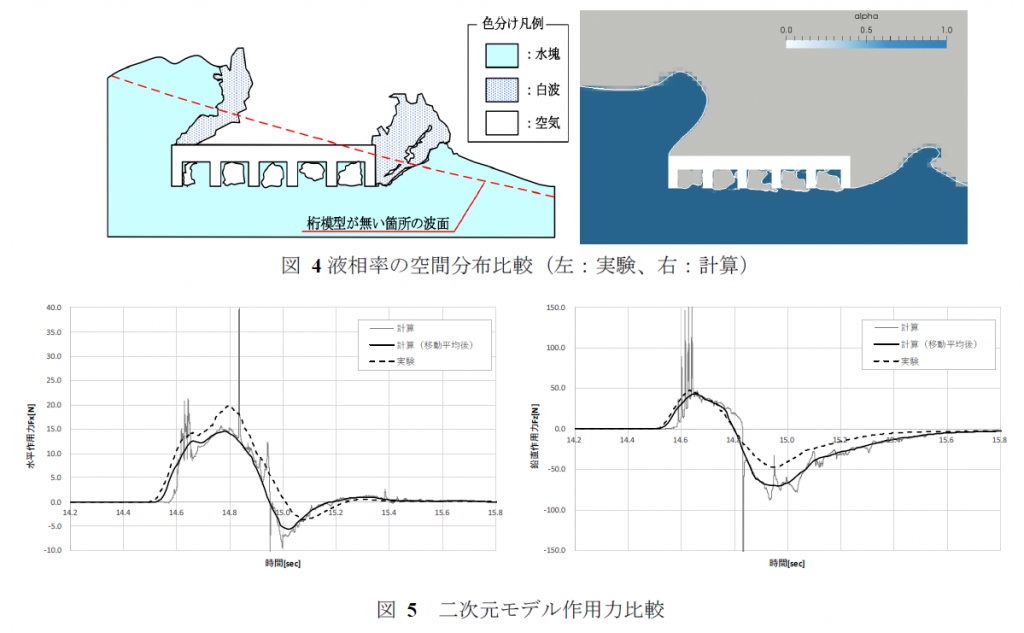
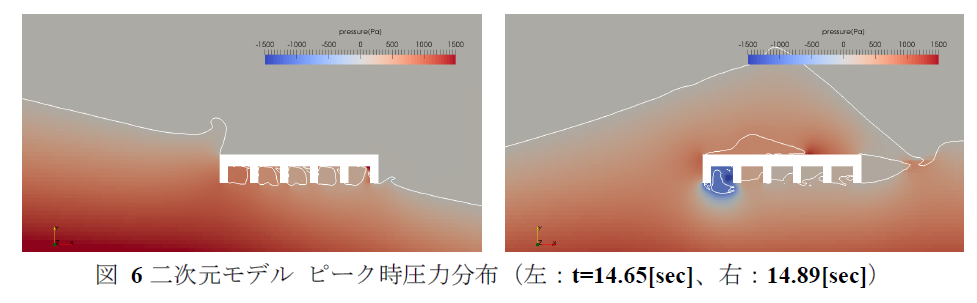
図 4に津波衝突時の液相の空間分布を示す。主桁間の液相分布や津波の波面など、実験と定性的に良い一致が見られる。図 5に橋桁への作用力の時刻歴を示す。黒実線は実験と同様に0.1[sec]の移動平均を施した結果である。移動平均後の結果を実験と比較すると、水平力・鉛直力ともに実験の傾向を概ね再現していることが分かる。ただし下向きの鉛直力に関しては、移動平均後の結果でも計算がやや過大に評価していることが分かる。また、移動平均前の計算結果では複数の作用力のピークが見られる。t=14.65, 14.89[sec]に着目し、各時間断面での圧力分布を図 6に示す。t=14.65[sec]では桁間で水面がせり上がることにより、橋桁を押し上げる大きな圧力が発生している。鉛直作用力の時刻歴では同様のピークが5点連続して見られるが、これは津波の進行方向側から順に、それぞれの桁間でせり上がりが発生するためである。t=14.89[sec]では津波先端部が落下した際に桁上面で大きな圧力が、そして桁内部で剥離による負圧が発生し、下向きの大きな鉛直力が作用する結果となった。本稿では二次元解析を実施したためこれらの作用力のピークが顕著にあらわれたが、実際の体系では時間的・空間的に分散し、作用時間も短いため測定は困難であると考えられる。また実験では橋桁と壁面の間に空隙が存在するが、本計算では奥行き方向に一様な体系を仮定したため、主桁間に発生する負圧を過大に評価したと考えられる。
参考:三次元解析による追加検討
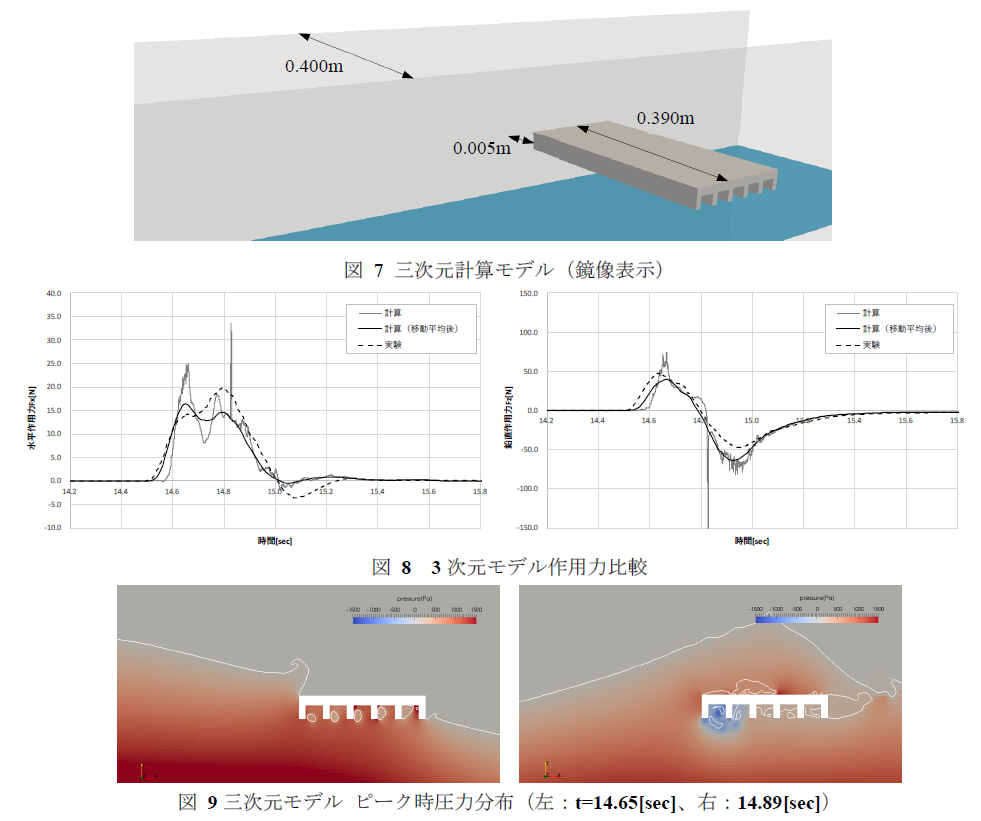
二次元によるモデル化の影響を確認するため、三次元解析を実施した。図 7に計算モデルを示す。水路の中心で対称境界を仮定し、実験と同様に橋桁と水路壁面の間には0.005mの空隙を設けた。
図 8に作用力の時刻歴を、図 9に圧力分布を示す。移動平均前の作用力のピークは二次元解析と比較して少なく、また大きさも小さくなっている。ピーク圧力の発生が時間・空間的に分散したためであると考えられる。また下向きの鉛直力の大きさは二次元解析と比較して低減し、実験と良い一致を示す結果となり、橋桁と水路壁面の空隙が結果に影響を与えていることが分かる。
参考文献
1) 田中将登,幸左賢二,佐々木達生,佐藤崇:橋梁に作用する孤立波の水平作用力評価,構造工学論文集,土木学会,Vol.61A,pp. 246-255,2015 年.
2) 田中将登,幸左賢二,佐々木達生,佐藤崇:孤立波性状の津波によって橋桁に生じる鉛直作用力特性の評価,土木学会論文集 B2(海岸工学),Vol. 71,No. 2,pp. I_973-I_978,2015 年.
3) 土木学会地震工学委員会 橋梁の対津波設計に関する研究小委員会: 対津波設計のベンチマークテストに関する論文集, http://committees.jsce.or.jp/eec209/system/files/proc_1.pdf
4) OpenFOAM Foundation, OpenFOAM Documentation, http://openfoam.org
5) Hansen, J. B. and I. A. Svendsen: Laboratory generation of waves of permanent form, Proc. 14th Conf. on Coastal Eng., 1974.


 (1 投票, 平均: 1.00 / 1)
(1 投票, 平均: 1.00 / 1)