前回の記事では課題1に対する弊社の数値計算結果を紹介したが、本記事では課題2に対する粒子法を用いた数値解析結果を紹介する。
課題 2 はゲート急開により発生させた津波の橋桁への作用力を求める問題である。橋桁は直橋および斜橋の2 つの設置パターンがあり、本課題では斜橋への作用力を推定する。
1.手法
SPH法やMPS法に代表される粒子法はメッシュを用いない計算手法であり,形状変化の激しい自由表面流れなどの流体解析や,大変形を有する固体問題等で幅広く利用されている.本解析では,対象とする橋梁付近の複雑な流れを3次元的に再現するため,SPH法を解析手法として選択した.SPH 法では次式で示されるように位置\(x\)における物理量\(ϕ(x)\)を着目粒子\(i\)の影響半径内の粒子物理量の重み付け和として表現する.
\begin{align*} ϕ(x) ≈〈ϕ_i 〉= \sum_{j}\frac{m_j}{ρ_j} ϕ_j W(r_ij,h) \end{align*}
\(mj\)と\(ρj\)はそれぞれ近傍粒子\(j\)の質量と密度であり,重みは粒子間距離\(r_ij\)と基準距離\(h\)の関数であるカーネル関数\(W(r_ij,h)\)により計算する.本研究においてはカーネル関数として5次のB-Spline関数を用い、初期粒子間距離の3倍を影響半径として計算を実施した.流体運動の基礎方程式には連続の式とNavier-Stokes方程式の2式を用いる.本解析では流体圧力を評価する際に,圧力ポアソン方程式を解く半陰的な解法 1)を用いることとし,計算の安定化を目的として,近藤ら 2)がMPS法に導入した生成項モデルをSPH法に適用した.
2.条件
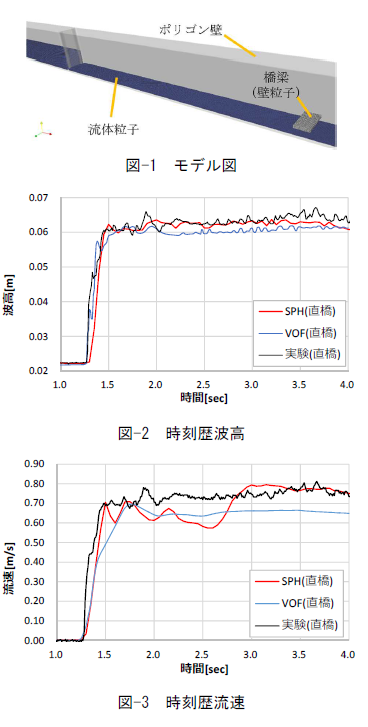
解析には実験の模型と同スケール,同形状の3次元モデルを用いる.橋梁模型は壁粒子,その他の壁面はポリゴン壁1)でモデル化し(図-1)、壁面の粘着条件はMorrisらの手法3)に従い非すべり条件を付与した.直橋斜橋ともに初期粒子間隔は5mm,時間増分1.0×10-4[s],総粒子数はそれぞれ593,050粒子,592,874粒子である.流体の密度は1,000[kg/m3], 粘性係数は0.001[Pa・s]とした.
3.結果
本概要では,上記のSPH法による解析結果(負圧を考慮しない)に加え,別途解析を実施したVOF法の結果(負圧を考慮する)を参考値として記載し,橋梁に対する津波作用力を実験と比較する.
はじめに,直橋模型前方で計測された波高変動と流速の比較を図-2,図-3に示す.ここで解析における波高は,観測点上に存在する水粒子の体積より算出し,流速は観測点の周囲に存在する水粒子の平均速度から求めた.同図より,実験の流速と比較して解析の流速に時刻暦の変化が見られる一方で,ほぼ同時刻に観測点に波が到達していることがわかる.
これは、本解析によって大局的な水の流れを再現することはできているものの,流速計が評価する局所的な流速を評価するための解像度が不足していたた め,両者に差が見られたものと考えられる.また波高に関しては,実験と解析の間に良好な一致が見られた.
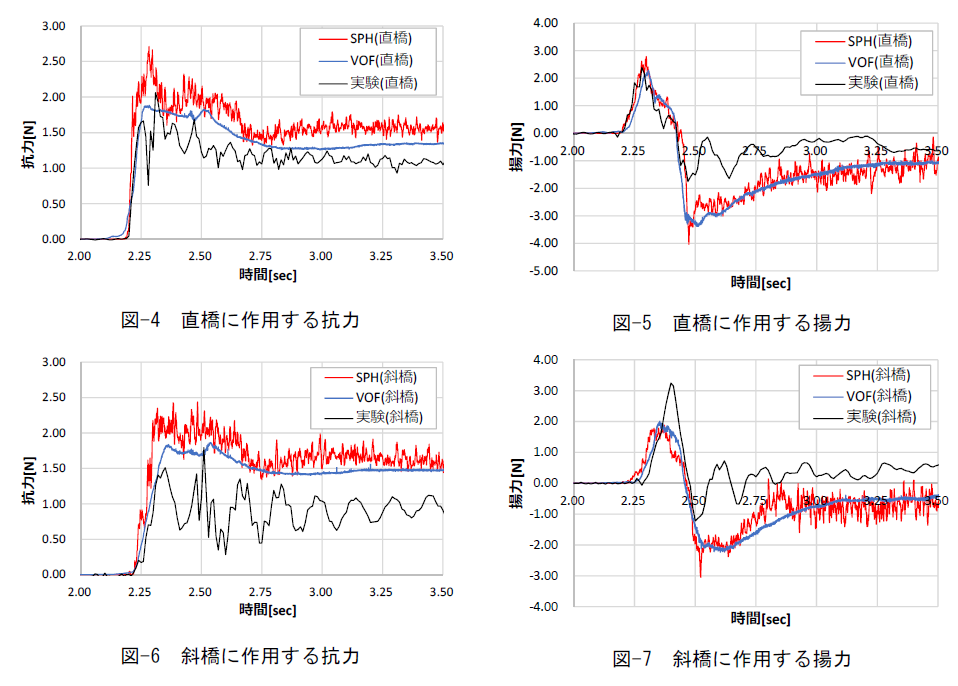
次に,直橋に作用する抗力と揚力の比較をそれぞれ図-4,図-5に示す.同図より,解析で観測された抗力は最大値で約31%大きく評価されているものの,おおむね実験と同様の傾向を示していることがわかる.同様に揚力に関しても,衝突後に上向きの力が作用し,その後下向きの力が作用するといった実験結果を再現していることが分かった.しかしながら,下向きの揚力値は最大値で2倍程度過大に評価されており,これは参考値として示したVOF法においても同様の結果が得られた.
最後に,斜橋に作用する抗力と揚力の比較をそれぞれ図-6,図-7に示す.斜橋では,流れ方向に対して斜めに模型が設置されているため,直橋に対して最大抗力の発生が遅れる現象が再現された.一方で直橋と同様に,抗力と揚力の最大値では,実験と解析の間に乖離が見られた.
中尾らの研究4)では,衝突する津波の形状や模型形状によって模型周辺に剥離が発生し,それによって生じる負圧が揚力に大きく影響すると報告されている.しかし,今回のモデルでは,津波作用力を評価する際に負圧を考慮していないSPH法と,負圧を考慮したVOF法の両解析に共通して,上述した傾向が観測されており,今回のモデルにおいて負圧は揚力に大きく影響しないものと予測される.ことから,各数値解析手法に共通して,再現できていな何らかの要因が,負圧以外に存在しているものと考えられる.
参考文献
1) 渡辺高志,桝谷浩,三橋祐太:壁面境界の大変形を考慮した粒子法の計算手法に関する基礎的研究,日本計算工学会論文集, No.20130021,2013.
2) 近藤雅祐,越塚誠一:MPS における不自然な数値振動の抑制,日本計算工学会論文集,No.20080015,2008.
3) J. P. Morris, P. J. Fox, Y. Zhu:Modeling Low Reynolds Number Incompressible Flows Using SPH, Journal of Computational Physics, 136, Issue 1, pp.214-226,1997
4) 中尾尚史,糸永航,松田良平,伊津野和行,小林紘士:基本的な断面形状の橋梁に作用する津波外力に関する実験的研究, 土木学会論文集A2(応用力学),Vol.67,No.2(応用力学論文集Vol.14),I_481-I_491,2011.


 (まだ評価がありません)
(まだ評価がありません)