Distinct element method (DEM) (個別要素法)は1971 年にP.A Cundall が岩石力学分野 を対象に開発した数値解析手法であり、現在は流体力学及び熱力学を含む様々な 現象を対象とした数値解析に利用されている。本記事では構造工学的な視点から DEM について簡単に説明する。
DEMはLagrange記述の離散化手法であり、接触する要素間の相互作用をばねやダッシュポットによってモデル化し、不連続性の変形領域を含む現象を簡単に解くことができる。下図にDEM の要素技術の特徴についてまとめて示す。
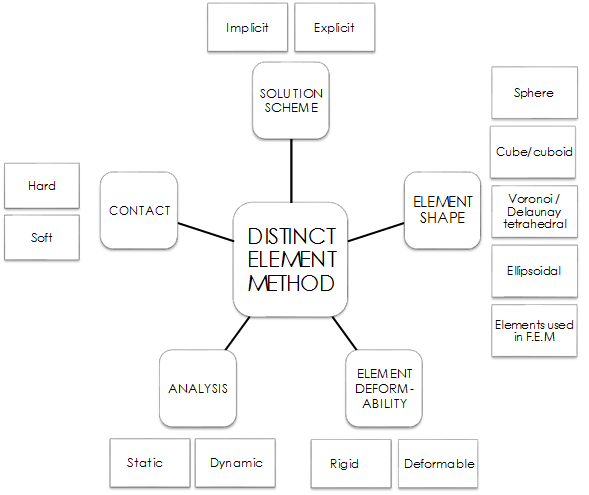
DEMの特徴
① 求解方法(Solution Scheme) :時間差分を陽解法もしくは陰解法で解く。一 般にDEM では陽解法が採用される。
② 要素形状(Element Shape) :円(2D)もしくは球体(3D)の要素形状がよく使 われるが、解析目的によっては他の形状でモデル化する。多面体や楕円体など の非球形状、粒子形状の集合体などが用いられる。有限要素が使用されることもある。
③ 要素の変形(Element Deformability):DEM では変形を考慮しない剛体(Rigid) 要素が一般に採用されているが、変形を考慮した要素を扱うことも可能である。差分法や有限要素法などを利用し、例えば、不連続変形法(Discontinues Deformation Method )や応用要素法(Applied Element Method)などの解析手法がある。
④ 解析の対象(Analysis): DEM では主に動的解析が行われている。これは陽解法の採用が一般的であり、静的解析にはあまり向かないことも理由である。
⑤ 接触のモデル方法(Contact): DEM の接触のモデル化方法は大きくは2 つに分類できる。 ソフトな接触モデルでは要素同士の重なりを許容し、重複によって生じるばね変位から接触力を求める方法であり、陽解法ベースのDEMでは一般的である。一方、ハードな接触モデルでは要素の重複を許容せずに計算を行うが、剛体の接触問題では多体同時接触を取り扱うことは出来ないため、接触が稀な現象などに対して適用される。なお、DDAのように形状変形を考慮する手法では、要素変形に転嫁することで要素重複を解消することも可能であり、反復計算処理を行うことによって重なりを許容しない接触モデルの一つと言える。
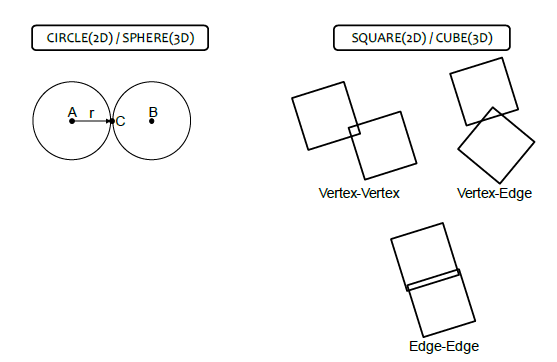
接触のモデル化
一般的なFEM とは異なり、DEM は時間ステップごとに要素の位置や姿勢を計算して、要素が接触しているか判定する。接触判定計算のアルゴリズムは、要素の形状によって異なり、複雑な要素を利用するとかなり計算時間がかかってしまう。よって、円形や球要素を利用する方法がよく採用されている。円形(2D)もしくは球体(3D)では、要素の位置と半径のみで接触判定ができる。以下の図に示すように、四角形等のブロック形状を用いる場合は、2 次元では接触のパターンが3 つあり、3 次元では接触パターンが12 個ある。
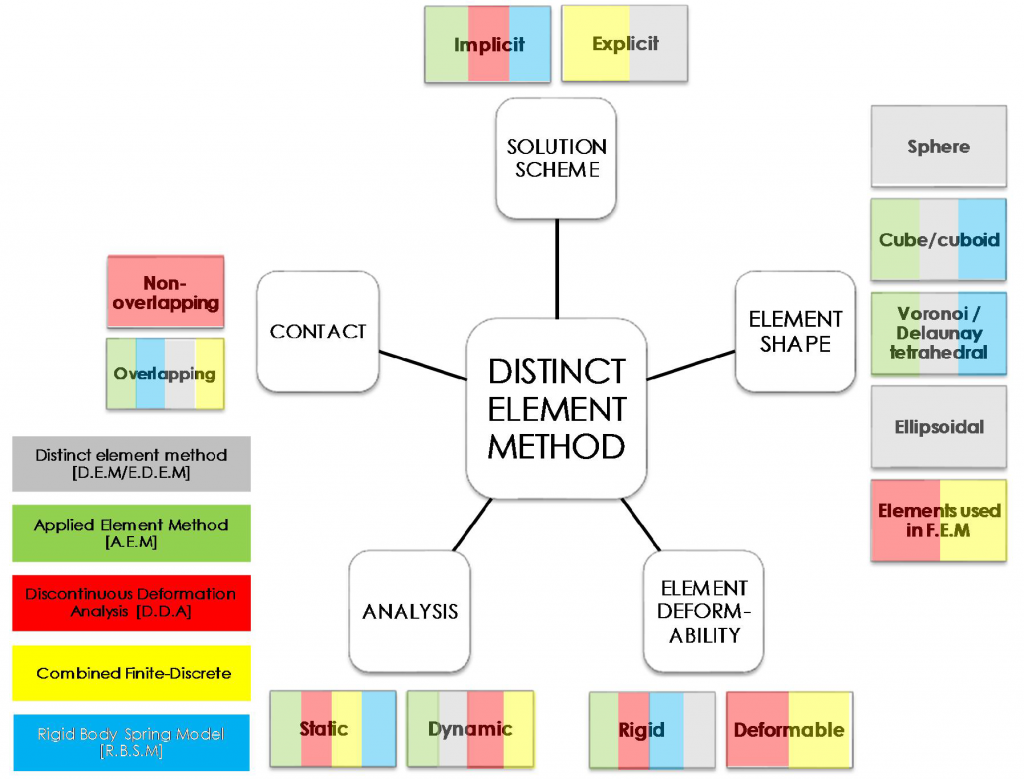
DEMに代表される不連続性の解析手法の分類
先述の解析手法の特徴を整理して、下図に不連続性の大変形構造解析に適用され
る様々な解析手法についてまとめた。図中の要素技術の色分けは対応する解析手法の凡例色を意味している。
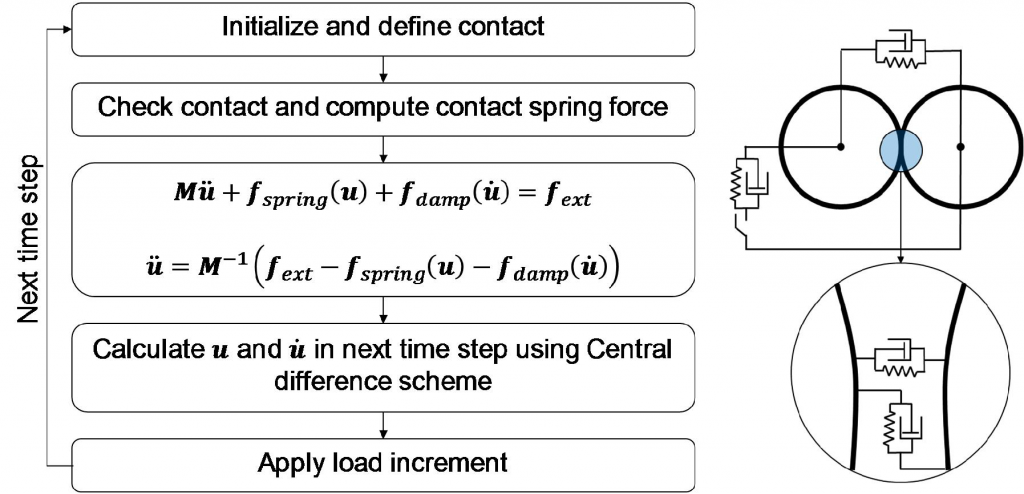
Distinct Element Method
これらの大変形解析手法の中でよく使われている手法はDistinct Element Method である。最も一般的なDEM では、剛な球体要素を使って、接触境界を鉛直及びせん断ばね(ダンパー)でモデル化する。下図に解析手法の流れを示す。
個別要素法のデメリットとしては、パラメータスタディが必要な(接触に関す
る)パラメータが多く、決定した値によって解析精度が変わることである。ま
た、個別要素法を連続体の構造解析に適用する場合、ポアソン効果を考慮することが一般に難しい。これはばね変形と作用力の向きが同じであり、多軸の連成を考慮しないためである。
構造解析分野では有限要素法(FEM)がよく使われているが、不連続性の変形領域を含む場合(例えば地盤すべり、構造物破壊、崩壊現象の解析)、一般的なFEM等の解析手法では、破壊の取り扱いや接触解法の収束性に問題が生じることが多く、頑強性の観点から個別要素法がよく使われている。


 (4 投票, 平均: 1.00 / 1)
(4 投票, 平均: 1.00 / 1)