1.目的
原子力発電所などに代表される安全上重要な施設・設備の基礎地盤や周辺斜面の安定解析においては,長年2次元解析による検討が行われてきた.同一な形状が連続する斜面など,2次元による検討が合理的である対象も多い一方,建屋の影響を受ける基礎地盤や複雑な形状を有する斜面においては3次元効果が無視できないものと考えられる.そこで本研究では,3次元斜面のFEMモデルに対して静的震度による解析を実施し,得られた応力場を用いてすべり面およびすべり方向を任意に決めた場合の安全率の算定を行い,3次元によるすべり安全率の検討を実施した.3次元すべり安全率の算出にはPOST-S/3D(構造計画研究所)を用いた.
2. 3次元のすべり安全率の計算方法
2次元モデルにおいてはすべり面が線として表現されるため,すべり方向などを定めることは容易である一方,3次元モデルを用いた場合はすべり方向の設定に任意性を有する.本研究では,すべり方向を固定し,以下の方法で3次元のすべり安全率を計算した.
コーシーの式より要素\(i\)の仮想切断面に働く作用力\(f_i\)は次式で計算できる.
\(f_i=σ_i n_i a_i\)
ここで,\(σ_i\)は応力テンソル,\(n_i\)は切断面の単位ベクトル,\(a_i\)は微小面積である.
仮想切断面で区切られた外側領域が剛体的に滑動すると考えると,各時間断面において不平衡力が生じている.ここで,作用力\(f_i\)は垂直抗力\(f_i^n\)と滑動力\(f_i^t\)に分解できる.
\(f_i^n=(f_i・n_i)n_i\)
\(f_i^t=f_i-f_i^n\)
滑動力の向きを考慮した場合,任意時間断面におけるすべり安全率S.F. は次式から計算できる.
\(S.F.= \frac{Σ|f_i^n| ・ tanϕ_i+C_i ・ a_i}{Σf_i^t ・ s_i}\)
ここで,\(C_i\)は要素\(i\)の粘着力,\(ϕ_i\)は内部摩擦角,\(s_i\)はすべり方向を表すベクトルである.
3. 2次元のすべり安全率との比較
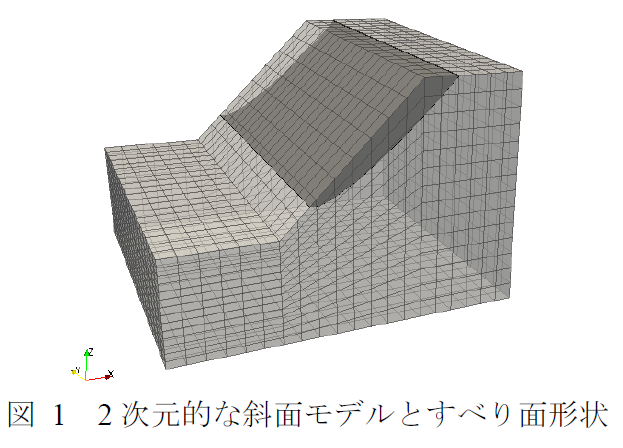
図 1に示す2次元的な斜面モデルおよびすべり面形状についてすべり安全率を算定し,2次元のすべり安全率と比較する.解析モデルは一様地盤とし,自重解析を実施する.すべり面を同一とした場合、2次元モデル,3次元モデルのすべり安全率は両方とも1.036となり,一致する結果となった.以上より,すべり安全率の計算方法および計算プログラムの妥当性が示された.
4. すべり面形状を変更した場合のすべり安全率
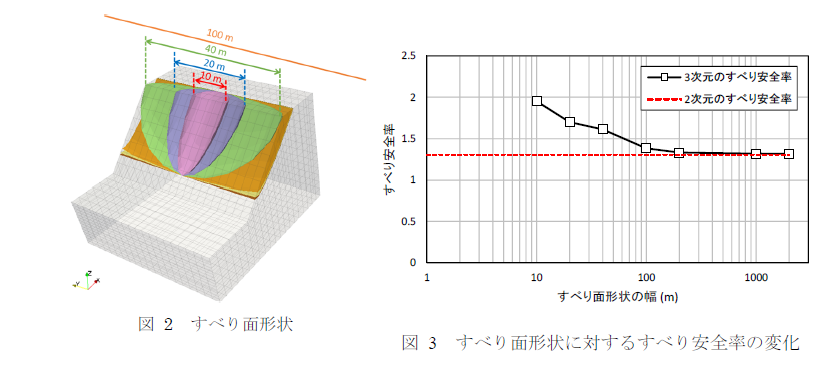
すべり面形状を変更することですべり安全率がどの程度変化するかを検討するため,図 2に示すようにすべり面形状の幅を徐々に広げてすべり安全率を算定する.
図 3にすべり面形状の幅に対するすべり安全率の変化を示す.すべり安全率は幅が広げる程小さくなり,2次元のすべり安全率に漸近することが分かる.
5. 凸型・凹型の斜面モデルの安全率の算定
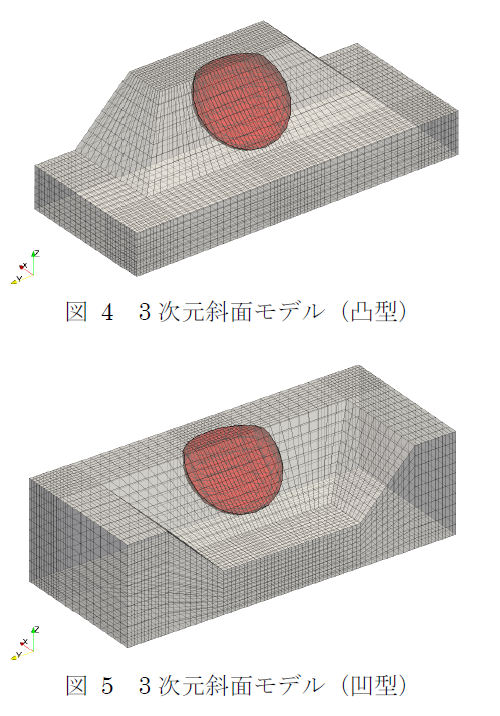
2次元的な斜面以外の斜面モデルを用いた場合にすべり安全率がどのように変化するかを検討するため,図 4および図 5に示す凸型および凹型の3次元斜面モデルを用いてすべり安全率を算定した.応力場は,自重および静的震度(KH=0.30,KV=0.15)を付与した静的解析によるものを用いた.
すべり面は楕円体を仮定し,楕円体の中心,半径(3成分),回転角のパラメータにより表現する.各パラメータの取る範囲を仮定し,総当たりで複数の楕円体に対して安全率を計算した.今回の計算では楕円体の法尻直交方向の中心は斜面の中央位置に固定した.求まった複数の安全率の最小値をモデルの最小すべり安全率とした.本検討では各モデルで約3万種類のすべり面による安全率計算を実施している.ただし,設定したすべり面の中には地表面をかすめるように通る面積の小さいすべり面も含まれる.これらのすべり面等は寄与が小さいとして除外して最小値を算出した.すべり方向は法尻方向とした.
計算により得られた凸型モデルの最小すべり安全率は0.91,凹型モデルの最小すべり安全率は0.98となった.最小すべり安全率となったすべり面を図 4および図 5に重ね描いて示す.凹型モデルにおいては斜面の両端が地盤によって拘束されているため,変形が小さくなることから安全率が大きめに評価されるものと考えられる.
6. まとめ
3次元斜面のFEMモデルに対して静的解析を実施し,すべり面およびすべり方向を任意に決めた場合の安全率の算定を行った.2次元的な斜面のモデルによるすべり安全率は2次元解析の結果と一致し,計算の妥当性が検証できた.さらに斜面の3次元形状を考慮した解析モデルですべり安全率を計算し,結果に差が出ることが確認できた.3次元で斜面およびすべり面形状をモデル化することで,より現実に即した斜面安定性評価が可能になると期待できる.
参考文献
金戸俊道ら:3 次元性を考慮した斜面の安定解析について,電力土木,No.296,16-21,2001.


 (1 投票, 平均: 1.00 / 1)
(1 投票, 平均: 1.00 / 1)