近年地中構造物等の地震時健全性評価などの観点から,地震時における断層の変位量の評価が求められている.断層の変位は震源断層の破壊から引き起こされるものであり,有限差分法や有限要素法などを用いた検討が行われている.本研究では,2014年11月22日に発生した長野県神城断層地震を対象として,非線形有限要素法を用いた動力学的シミュレーション解析を実施した.地盤をソリッド要素,断層面をジョイント要素によりモデル化した.長野県神城断層地震は神城断層の一部とその北方延長を震源とする逆断層型地震であり総延長9km,最大1m程度の地表断層変位が確認されている.断層に初期応力を与え,震源を意図的に破壊させることで破壊の伝播解析を実施し,解析で得られた断層変位量および応答時刻歴を観測記録と比較した.この際大規模モデルを解析可能な有限要素法コードFrontISTRにGoodmanらによるジョイント要素を拡張した要素を導入した上でシミュレーション解析を実施した.
1.はじめに
近年,地中構造物等の地震時健全性評価などの観点から,地震時における断層変位量の評価1)が求められている.断層の変位は震源断層の破壊により引き起こされるものであり,有限差分法2)3)や有限要素法4)5)を用いた検討が行われてきた.特にすべり弱化モデルを用いて断層の自発的破壊過程を再現した動力学的シミュレーションは,有限差分法を中心に数多くの研究が行われている2)3).
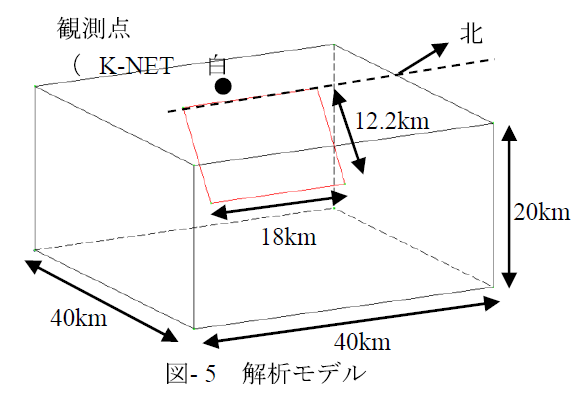
本研究では,2014年11月22日に発生した長野県神城断層地震を対象として,3次元非線形有限要素法によるシミュレーション解析を実施した.長野県神城断層地震(M6.7,Mw6.2)は神城断層の一部とその北方延長の長さ約20km,深さ約10kmを震源断層とする逆断層型地震であり,総延長9km,最大1m程度の地表断層変位が確認されている9)10)11).また,断層近傍のK-NET観測点において最大600Gal程度の加速度が観測されている.震源断層を含む40km×40km×20kmの領域を地盤をソリッド要素,断層をジョイント要素によりモデル化した.断層の破壊過程を応力降下を取り込んだ非線形構成則によりモデル化し,初期条件としてジョイント要素に初期応力を与えることにより断層の破壊を発生させ,破壊の伝播により発生する地表面の応答時刻歴をK-NETの観測記録と比較した.また,地震後の現地調査により観測された地表断層変位を解析により得られた変位量と比較した.本研究は大規模モデルを並列計算可能な有限要素法コードFrontISTR6)を用いて実施した.これにより広域地盤を比較的細かいメッシュにより解析することが可能となった.そこで用いるメッシュの細かさが解析結果に与える影響も合わせて検討した.
2. 3次元有限要素法による解析条件
(1) ジョイント要素による断層のモデル化
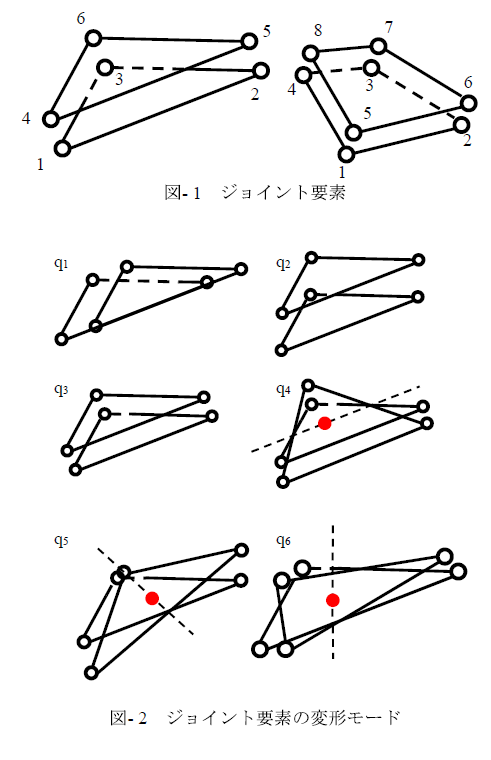
本研究では断層を図- 1に示すジョイント要素によりモデル化した,ジョイント要素とは2物体の接触/滑動/剥離を簡易的に模擬した有限要素であり,Goodman12) の提案するものや3次元アイソパラメトリック要素を基にして定式化したものなどいくつか提案されている.Goodmanらによるものは形状を長方形に仮定し,接触する2面の間の変形を図- 2に示す6つのモードの組み合わせで表現したものである.筆者らはこれを任意形状の3角形もしくは4角形に拡張し,FrontISTRに実装した.これにより,ゆがんだメッシュでも精度の高い解析が可能になった.
本研究で用いる断層面のせん断応力‐相対変位関係を図- 3に示す.ジョイント要素は面内の並進変形に対して2方向の自由度を有するため(図- 2の\(q_1\)および\(q_2\)),せん断応力\(τ\)および相対変位\(ε\)を式(1)および式(2)により評価する.ただしここで\(f_{q1}\),\(f_{q2}\)はそれぞれ\(q_1\),\(q_2\)のモードによるせん断力,\(δ_{q1}\),\(δ_{q2}\)は\(q_1\),\(q_2\)のモードの変位量(食い違い量)である.
\(τ=\sqrt{{f_{q1}^2}+{f_{q2}^2}} \)
\( ε=\sqrt{{δ_{q1}^2}+{δ_{q2}^2}} \)
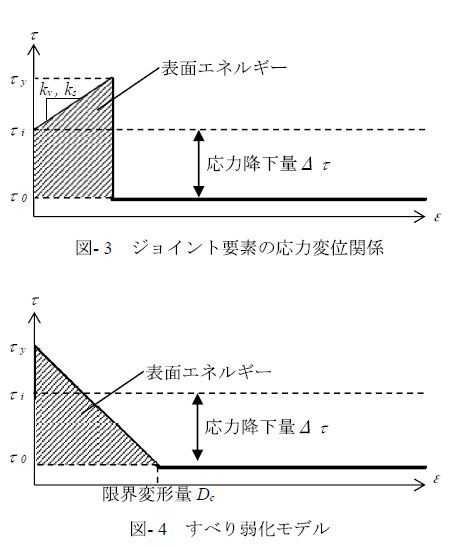
ジョイント要素は図- 3に示すように,せん断応力\(τ\)が降伏応力\(τ_y\)に達した時点ですべり破壊を生じ,\(τ_0\)までの応力降下を生じる.既往の研究7) によるとすべり破壊後の挙動は,急激に\(τ_0\)まで降下するのではなくある程度の傾斜を持っており,有限差分法におけるすべり弱化モデルでは図- 4に示すような限界変形量\(D_c\)まで線形に低下するモデルがよく用いられる.本研究では簡便のためすべり破壊が生じた瞬間に\(τ_0\)まで応力降下するモデルを採用した.また,既往の研究4) によると解析結果は \(Δ_τ=τ_y-τ_0\)の相対量に依存し\(τ_0\)の絶対量には依存しない.そこで本研究では\(τ_0\)=0MPaとして,相対量\(Δ_τ\)に着目した解析を実施した.さらにジョイント要素の初期せん断剛性ksは壇ら2)を参考に,すべり弱化モデルにおける\(D_c\)=25cmから計算される表面エネルギーが同等になるように定め,鉛直剛性\(k_v\)は線形で十分剛な値とした.
(2) 運動方程式
運動方程式は式(3)により与えられる.
\(Mẍ+Cẋ+Kx=F-Q\)
ここでxは変位,M,C,Kはそれぞれ系の質量,減衰,剛性マトリックス,Fは外力ベクトル,Qは非線形に係る残差ベクトルである.減衰に関しては剛性比例型減衰を採用し,モデルの最大透過振動数と水本らの研究4)を参考に1Hzで2%の減衰となるように定めた.また地表面を除くモデル外周部に粘性境界を設定することにより反射波の影響を除去した.図- 3に示したジョイント要素の構成則により本問題は非線形性を持つためNewton-Rapson法による収束計算を実施した.
3. 解析モデル
解析に用いるモデルを図- 5に,断層パラメータ表- 1に示す.断層形状は産業技術総合研究所の活断層データベース13) および余震分布等 10)を参考に設定し,走向12度,傾斜50度,長さ18km,深さ10km(幅12.2km)とした.地盤の物性値は一般的に用いられる値としてせん断弾性係数\(μ\)=30GPa,単位体積重量\(γ\)=2.5t/m3としポアソン媒質(\(ν\)=0.25)を仮定している.本震の震源記録を参考に深さ5kmの位置に震源を設定し,当該位置のジョイント要素の\(τ_y\)を大きく設定し,設定した\(τ_y\)を超える初期応力を傾斜方向(縦ずれ方向)に設定することで解析開始と同時に破壊が始まるような条件となっている.断層面の形状に関しては断層北側で地表面変位が観察されていないことなどから実際は単純な矩形でないことも考えられるが,本検討では簡便のため矩形断層とした.
応力降下量は解析の最終状態における各要素の食い違い量\(Δu\)より断層面を\(Σ\)として式(4)および(5)を用いて計算されるモーメントマグニチュード\(Mw\)が実際の地震において観測された値と近くなる条件として一律1MPaを設定した.\(τy\)はAndrew 7)を参考に式(6)より定めた.
\(M_0=∫_Σ μΔudS\)
\(Mw=\frac{2}{3}log_{10} M_0 - 6.1\)
\( τ_y = 1.6Δ σ \)
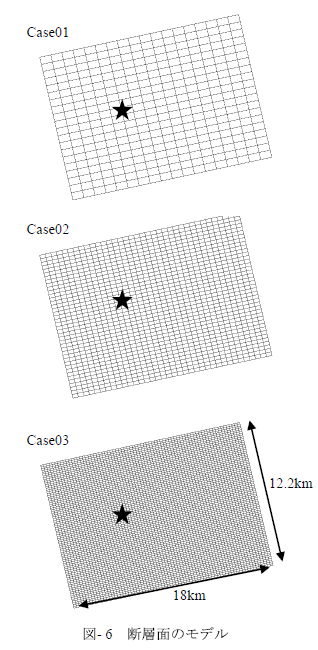
解析はメッシュサイズを変えた3モデルに対して実施した.基本となるCase01はジョイント要素の一辺の長さ\(Δ\)Lが最大1kmになるように定めている.基本となるモデルを倍に分割することにより細かいメッシュを,それをさらに分割することにより,より細かいメッシュを生成した.生成したモデルの一覧を表- 2にまとめる.表中の最大透過振動数 \(f_{max}\) は式(7)において\(n\)=4として計算した値である.ただし\(β\)はせん断波速度である.メッシュサイズを変えた解析を実施することにより,解析結果のメッシュサイズ依存性を合わせて検討する.
\(f_{max}=\frac{β}{nΔL}\)
解析はNewmark-\(β\)法(パラメータ\(β\)=0.25,\(γ\)=0.5)による逐次非線形動解析により実施し,解析の積分時間刻み\(Δt\)=0.01(s),継続時間\(T\)=10(s)とした.

4. 解析結果
解析結果を示す.ただしモデル変形図,断層破壊時刻,断層食い違い量,変位時刻歴は各解析モデルで大きな差異がみられなかったことより,代表ケースとしてCase02のもののみを示す.
(1) モデル変形図
解析最終時間断面の変形図を図- 7に示す.
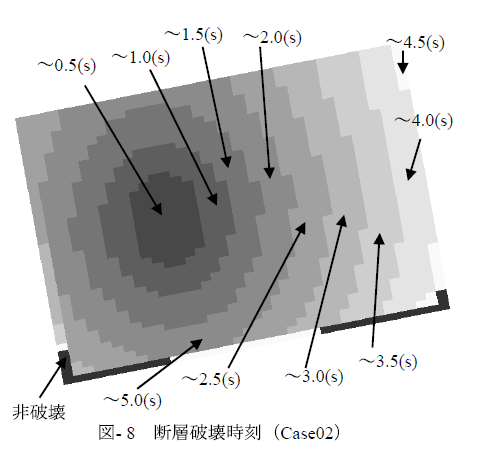
(2) 断層破壊時刻
断層面状の各ジョイント要素が破壊した時刻をコンター図で示したものを図- 8に示す.図- 8より平均的な破壊伝播速度\(Vr\)は秒速3kmと評価され,地殻のS波速度\(β\)=3.46(km/s)に対して,\(Vr /β\)=0.87である.レシピ8)によると一般的な\(Vr\)と\(β\)の比は0.72であるが,それより大きい値が得られているとの記述もあり,本検討の結果は大きく現実と乖離するものではないと考えられる.また,破壊時に要する表面エネルギーを変えることで破壊伝播速度が増減することを確認している.
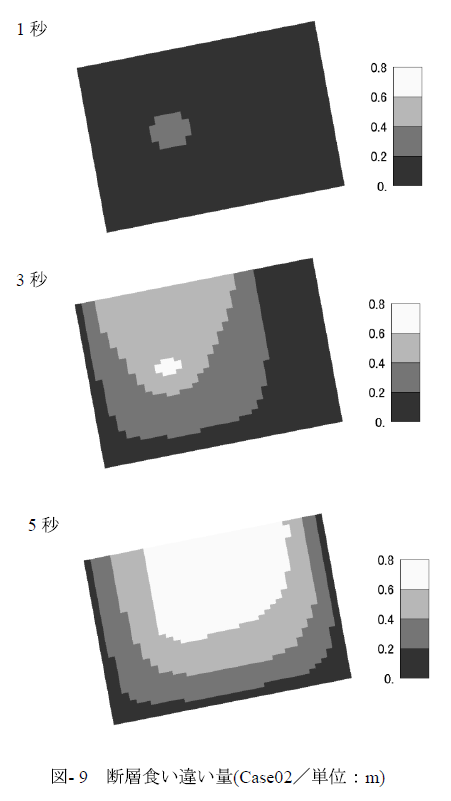
(3) 食い違い量
解析最終時間断面におけるジョイント要素に生じた食い違い量のコンター図を図- 9に示す.最終時間断面の食い違い量から計算される地震モーメントM0は2.94×1018(N・m)であり,これから計算されるモーメントマグニチュードMwは6.2である.実際の地震において気象庁から発表されたCMT解析の結果は地震モーメント2.98×1018 (N・m),モーメントマグニチュード6.2であり,よく一致した結果となっている.
さらに最終時間断面の地表面における断層食い違い量は80cm程度となっており,地震後に実際に計測された上下変位量は90cm程度であることから,解析は実際の現象をよく模擬できているものと考えられる.

(4) 応答時刻歴
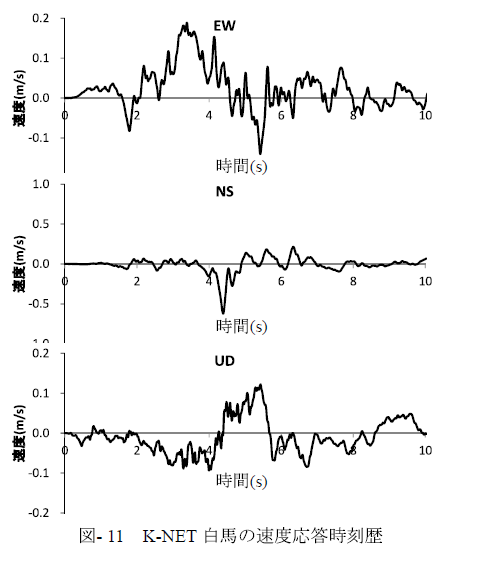
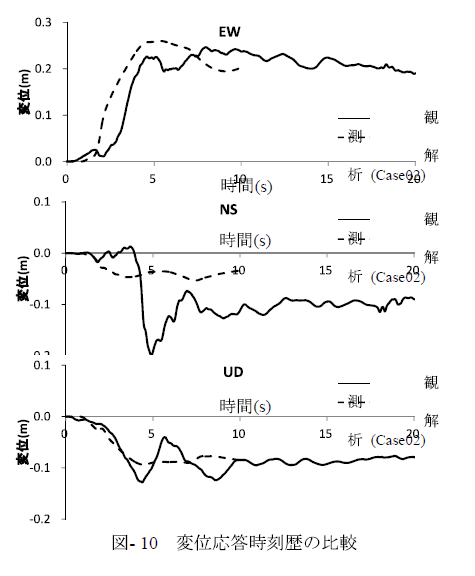
観測点位置における応答時刻歴をK-NET白馬で実際に観測された結果と比較する.本検討はモデルのメッシュサイズから計算される最大透過振動数が数Hz程度となり,比較的長周期の結果に着目するため時刻歴は変位および速度時刻歴を比較することとした.K-NET白馬の加速度応答時刻歴をBooreら15)の方法を用いて補正し,時間積分して求められる変位および速度時刻歴波形を解析で得られた波形と比較した.観測記録から求めた変位時刻歴をCase02の解析結果と比較したものを図- 10に,観測記録から計算した速度時刻歴を図- 11に,3モデルによる解析結果の速度時刻歴を図- 12に示す.ただし時間軸原点は適宜調整している.また観測の変位時刻歴は最終的な変位量を示すために20秒までの結果を示している.
K-NET白馬の観測点は断層の比較的近傍にあるため,解析最終時間断面で比較的大きな永久変位が生ずる結果となっている.EWおよびUD方向で最終的な変位量は0.2,-0.1(m)程度であり解析と観測でよく一致している.また細かい差異は見られるものの時刻歴としてもトレンドをよくとらえた結果となっている.一方NS方向の変位時刻歴は2~3倍程度の差異が生じており,解析の方が小さく評価された.
速度時刻歴においては振動の幅に着目すると観測記録ではEW,NS,UDでそれぞれ0.3,1.0,0.2m/s程度であるのに対し,解析では0.2,0.1,0.06m/s程度であり,こちらもNS方向での差異が大きくなる結果となった.
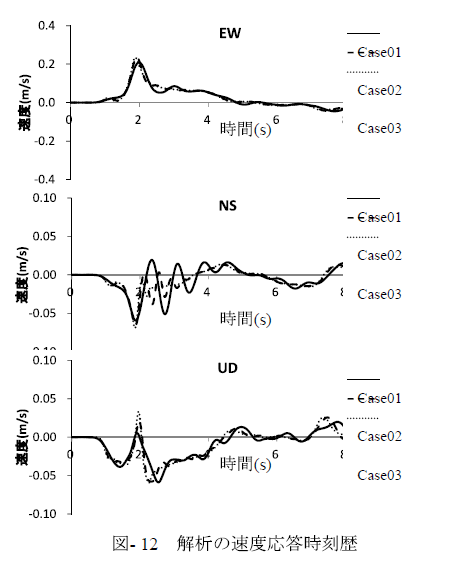
NS方向は断層面に沿った方向であり,単純な逆断層の破壊過程ではEW方向の方が応答は大きくなるものと予想される.気象庁発表のCMT解14)によると神城断層地震は20%程度の非D.C.成分を持っており,また本地震は左横ずれを伴うものであるという指摘16)も見られることから,断層の破壊過程はより複雑であるものと推測できる.
解析モデルのメッシュ分割数を増加させると,急激な速度変化が現れるようになるが,観測記録にみられるような複雑な振動を模擬できるようにはならない.この振動を模擬するためには,アスペリティに代表されるような局所的な構造や物性値のばらつきをモデル化する必要があるものと考えられる.
5. おわりに
長野県神城断層地震を対象とした断層の動力学的シミュレーションを有限要素法により実施した.応力降下量\(Δσ\)を調整することで,実際の地震における地震モーメントに近い結果となる解析結果を得ることができ,地表断層変位量およびNS方向以外の変位時刻歴も観測によく一致する結果となった.応答速度時刻歴に関しては,振幅は比較的近い結果となったものの有限要素メッシュを細かくしても実際の速度時刻歴波形に近い結果は得られなかった.
今後はより詳細な断層形状や物性値のばらつきなどを取り込んだより検討を実施していきたいと考えている.
謝辞:本研究では地震観測記録として(独)防災科学研究所によるK-NET強震記録を使用した.ここに記して謝意を表する.
参考文献
1) 一般社団法人原子力安全推進協会敷地内断層評価手法検討委員会:原子力発電所敷地内断層の変位に対する評価手法に関する調査・検討報告書,平成25年9月.
2) 壇一男,武藤真菜美,鳥田晴彦,大橋泰裕,加瀬祐子:動力学的シミュレーションによる断層の連動破壊に関する基礎的研究,活断層・古地震研究報告,No.7,259-271,2007.
3) 入江紀嘉,壇一男,生玉真也,入倉孝次郎:地中震源断層と地表地震断層の断層パラメータ間の経験的関係を拘束条件とした動力学的断層破壊モデルの構築-強振動予測のための運動学的断層モデルの高度化をめざして-,日本建築学会構造系論文集,Vol.75,No.657,1965-1974,2010.
4) 水本学千,坪井利弘,三浦房紀:3次元FEMによる断層モデルの解析に関する基本的検討,土木学会論文集,No.780,I-70,27-40,2005.1.
5) 水本学千,三浦房紀,坪井利弘:3次元有限要素法による2000年鳥取県西部地震の断層運動シミュレーション,第26回地震工学研究発表会講演論文集,2001年8月.
6) FrontISTR研究会HP: http://www.multi.k.u-tokyo.ac.jp/FrontISTR/ ,平成27年5月19日閲覧
7) D.J.Andrews:Rupture velocity of plane strain shear cracks,Journal of Geophysical Research,Vol.81, pp.5679-5687,1976.
8) 震源断層を特定した地震の強振動予測手法(「レシピ」),地震調査研究推進本部地震調査委員会(2009b),平成21年12月21日改訂.
9) 長野県北部地震に伴う地表変形調査,http://www.gsi.go.jp/cais/topic141203.html,国土地理院, 平成27年5月19日閲覧.
10) 長野県北部の地震活動,http://www.jishin.go.jp/main/chousa/major_act/act_2014.htm#a20141122,文部科学省研究開発局地震・防災研究課地震調査研究推進本部,平成27年5月19日閲覧.
11) 長野県北部の地震[2014年11月22日], https://www.gsj.jp/hazards/earthquake/naganokenhokubu2014/index.html,国立研究開発法人産業技術研究所地質調査総合センター,平成27年5月19日閲覧.
12) Goodman, R.E.:Methods of geological engineering in discontinuous rocks,West Publishing Company,Ch. 8,pp. 300-368,1976.
13) 活断層データベース,https://gbank.gsj.jp/activefault/index_gmap.html,産業技術総合研究所,平成27年5月19日閲覧.
14) 2014年11月22日22時08分 長野県北部 M6.7,http://www.data.jma.go.jp/svd/eqev/data/mech/cmt/fig/cmt20141122220817.html,気象庁,平成27年5月19日閲覧.
15) David M. Boore,Christopher D. Stephens,William B. Joyner:Comments on Baseline Correction of Digital Strong-Motion Data: Examples from the 1999 Hector Mine, California, Earthquake,Bulletin of Seismological Society of America,Vol.92,No.4,pp1543-1560,2002.
16) 日本地震工学会:2014年長野県北部の地震に関する調査団報告,2015.


 (1 投票, 平均: 1.00 / 1)
(1 投票, 平均: 1.00 / 1)