対津波設計のベンチマークテスト（３）-斜橋に対する津波作用力（VOF法による数値計算）

更新日：2020年9月14日

　前回の記事では課題2に対する粒子法を用いた数値計算結果を紹介したが、本記事では課題2に対するVOF法を用いた数値解析結果を紹介する。

　課題 2 はゲート急開により発生させた津波の橋桁への作用力を求める問題である。橋桁は直橋および斜橋の2 つの設置パターンがあり、本課題では斜橋への作用力を推定する。

１．手法

　水および空気を非圧縮性粘性流体と仮定し、気液二相流の数値流体解析により橋梁に作用する外力を推定した。解析コードは数値流体力学ツールボックスOpenFOAM¹⁾の標準ソルバの一つinterDyMFoamを用いた。空間の離散化には有限体積法、気液界面の捕捉にはVOF（Volume of Fluid）法、圧力-速度連成手法にはPIMPLE法、乱流モデルとして標準\(k-ϵ\)モデルを適用した。またAMR（Adaptive Mesh Refinement）により、気液界面の近傍で局所格子分割を行った。

２．条件

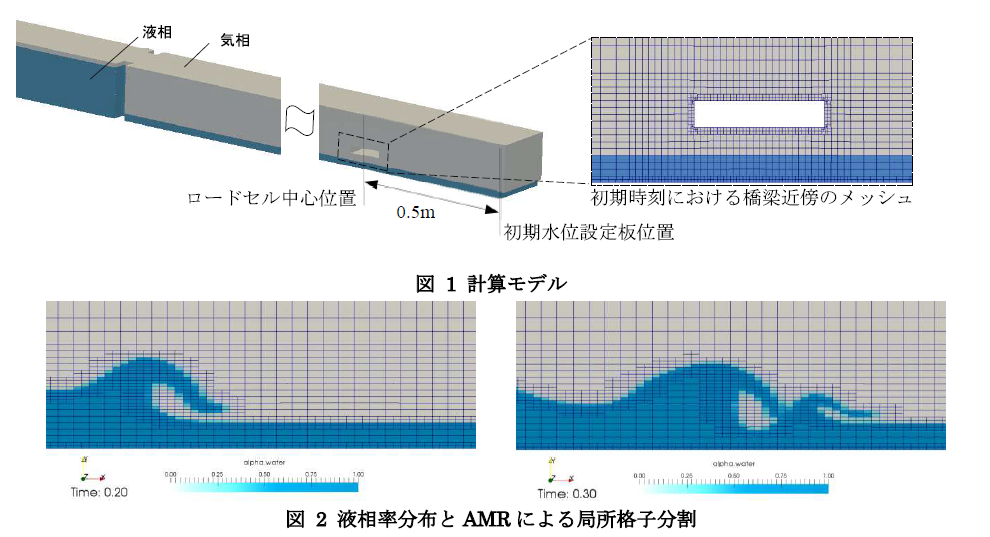
　図 1に計算モデルを示す。実験ではロードセル中心から1.5mの位置に初期水位設定板を設置しているが、計算では波力評価に影響しないと考えられるため、ロードセル中心から0.5m位置に初期水位設定板を設置し、領域を省略した。また実験では直橋・斜橋いずれもロードセルで片持ち梁的に模型を支持しているが、計算モデルでは両端に支持されるよう簡略化した。橋梁近傍での格子幅が0.002m～0.005mとなるよう非構造格子でメッシュ分割を行ったところ初期時刻での格子数は約32万となり、局所格子分割によって橋梁への衝突時には80万程度の格子数となった。

　橋梁および水槽との壁境界はノンスリップ条件とし、津波の流出部では速度について勾配0条件を与えた。解析再現時間はt=0.0～4.0の4.0秒間とし、t=0.0においてゲートは完全に引き上げられた状態とした。

３．結果（直橋）

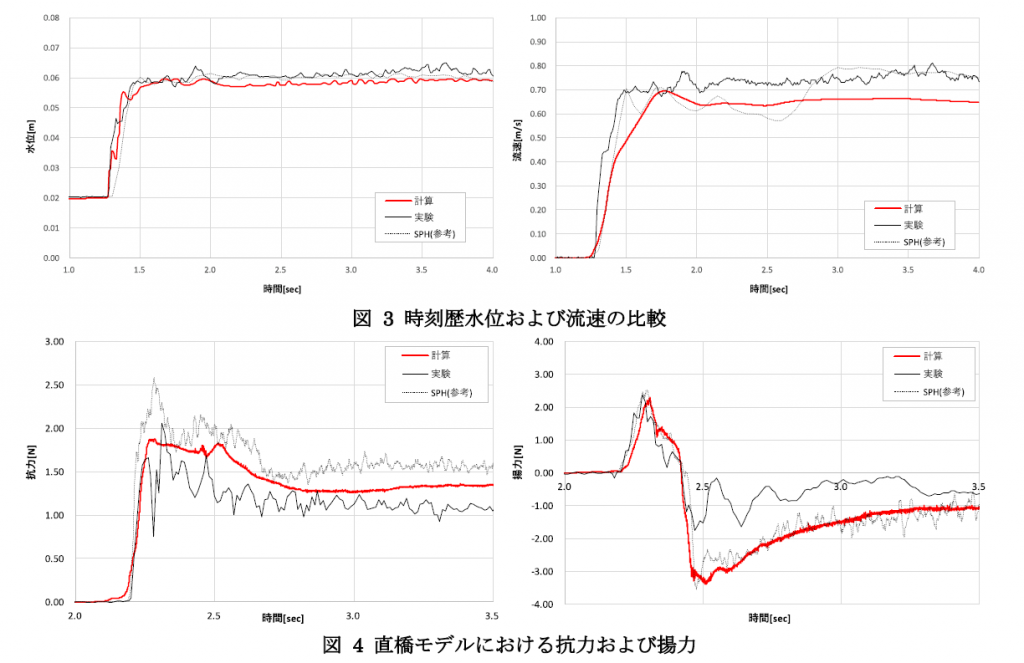
　橋梁の模型前方で計測された水位変動と流速の比較を図 3に示す。参考として、別途行ったSPHによる計算結果を破線で示す。流速はやや小さく評価しているものの、波の到達時間、水位ともに実験と良い一致が見られる。

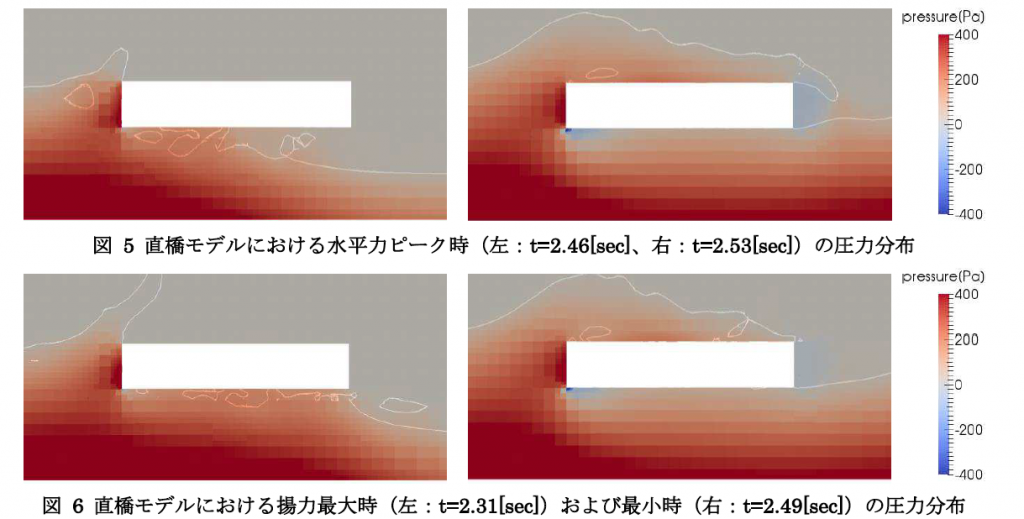
　直橋模型を対象としたモデルに関して、抗力と揚力の比較を図 4に示す。同図より，計算では実験よりやや大きい抗力が得られた。実験では流下方向に一定周期の振動がみられることから、実際には橋梁模型が振動していると考えられ、壁面と剛結合された計算結果が実験を上回る結果は定性的に正しいと言える。参考として示したSPHの結果も本計算と同様の傾向を示している。抗力は波の到達時t=2.46[sec]で最大となった後に緩やかに減少していくが、t=2.53[sec]付近で僅かに作用力が上昇する。これは橋梁背面で発生する負圧の影響（図 5）である。揚力に着目すると、上向きの揚力は実験を良く再現しているが、下向きの揚力に関しては実験との乖離が見られる。ただしSPHも同様の傾向がみられることから、計算で再現できない実験特有の条件があると考えられる。揚力最大・最小時の圧力分布（図 6）を確認すると、揚力の最大値は模型下面から作用する水圧が、最小値は模型上面から作用する水圧が支配的で、負圧はほぼ寄与していないことが分かる。参考値として示したSPHの結果は負圧を考慮していないが、抗力・揚力ともに本結果と近い値を示す

４．結果（斜橋）

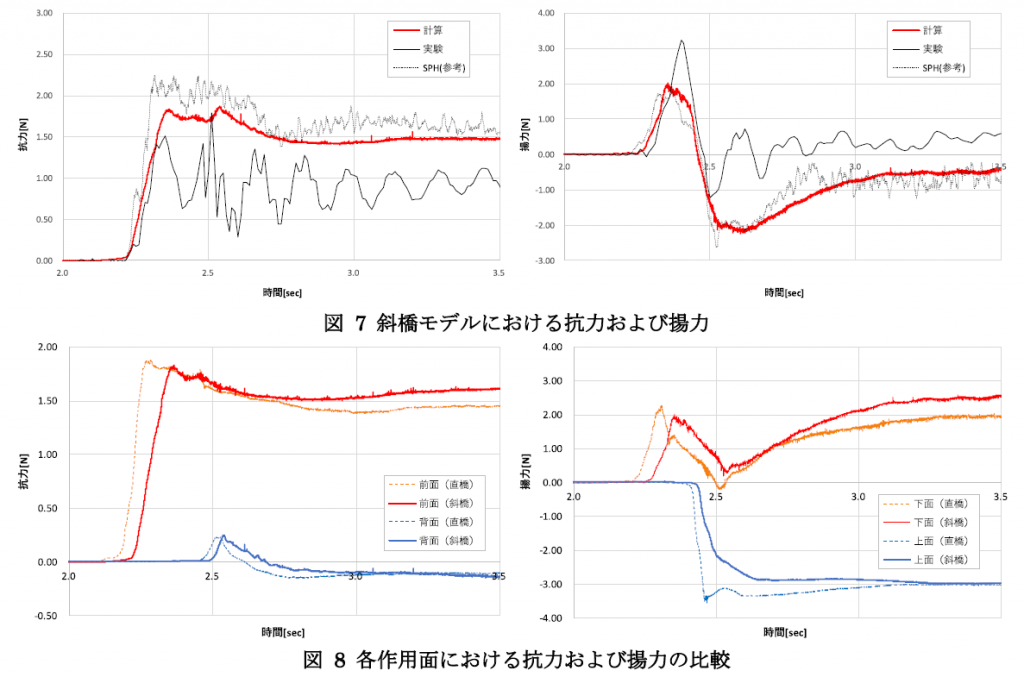
　図 7に斜橋模型における作用力の時刻歴を示す。抗力に関しては直橋モデルと同様、計算が実験より作用力を大きく評価し、SPHでも同様の傾向が得られている。揚力に関しては上向き・下向きともに実験と乖離が見られるが、本計算とSPHの結果は定量的にも一致している。実験の作用力の波形を確認すると、抗力・揚力ともに大きな振動が見られ、剛結合を仮定した計算結果と乖離したと考えられる。

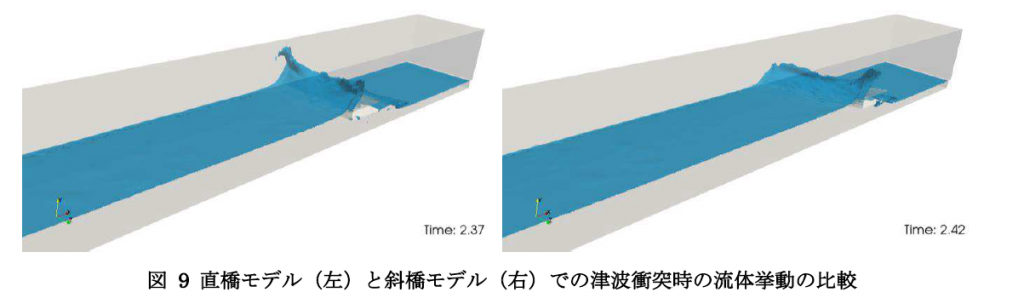
　図 8に、各モデルにおける作用面ごとの抗力・揚力を比較した結果を示す。定常的な流体力が作用するt=3.0[sec]以降は、抗力は作用面積が大きい斜橋モデルが直橋を上回る。一方、津波先端部が衝突するt=2.3[sec]付近では、作用面積が小さい直橋モデルへの抗力が斜橋を僅かに上回る結果となった。これは斜橋モデルでは津波到達時に波が時間的・空間的に分散して作用するためで、作用力の立ち上がりも斜橋モデルの方が緩やかであることが分かる。また図 9に津波衝突時の流体挙動を示すが、やはり直橋モデルの方が波のせり上がり高さが大きく、t=2.47[sec]付近で直橋モデルの上面で見られる下向き揚力のピークは、せり上げられた流体が落下した際に発生したものである。