3次元FEMによるすべり安全率の評価

更新日：2020年9月14日

　現在，原子力発電所の敷地内にある斜面や建屋直下の地盤は周辺斜面や基礎地盤と呼ばれ¹⁾，その耐震安定性評価は有限要素法（以下，FEM）に基づく安定性評価が行われることが一般的です．別途，FEMを用いた常時解析と地震応答解析を実施しておき，それらの応答結果を用いて想定すべり面に対する安定性を評価するという方法です．常時解析や地震応答解析は2次元FEMに基づくことが一般的ですが，2次元モデルの場合，奥行き方向には同じ断面が続くという仮定が入りますので，実際の3次元的なすべり面形状で期待される側方の拘束効果がなく，すべり安全率が安全側に評価されることになります．昨今ますます原子力発電所の安全性が求められる中で，評価用の地震動も大きくなっているのが現状です．よって，これまでの2次元モデルによる評価では評価基準値を満たさないことも考えられます．そこで本文では，3次元FEMに基づくすべり安全率の算定に関する解析事例をご紹介します．3次元FEMにより，これまで2次元モデルを用いて実施してきた評価をより合理的に、精度良く評価することが可能となります．

1. 3次元FEMに基づくすべり安全率

1.1 すべり安全率の計算方法

　3次元FEMに基づくすべり安全率を算定するためには，予め3次元の応力状態が必要です．本文の冒頭に示した原子力分野では，地震時の安定性に関する評価を行うことが多いため，地震応答解析結果として得られる3次元の応力状態を用いることとなります．以下，応力状態が既知であると仮定し，それ以降からすべり安全率の算出までの流れを示します．

　コーシーの式より地盤内部の仮想切断面\(i\)に働く作用力\(f_i\)は式(1)で計算できます．

\( f_i =σ_i n_i a_i\)

　ここで，\(σ_i\)はコーシー応力テンソル，\(n_i\)は切断面の単位法線ベクトル，\(a_i\)は切断面の面積を示しています．
　連続する仮想切断面で区切られた外側領域が剛体的に滑動すると考えると，切断面には各時間断面において不平衡力が生じています．ここで，作用力\(f_i\)は垂直抗力\(f_i^n\)と滑動力\(f_i^t\)に分解できます（式(2)(3)参照）．

\(f_i^n=(f_i・n_i)n_i\)

\(f_i^t=f_i － f_i^n\)

　以上より，滑動力の向きを考慮した場合，任意時間断面におけるすべり安全率S.F. は式(4)から計算できます．

\(S.F. = \frac{|f_i^n|・tanϕ_i +G_i・ a_i }{Σf_i^t・s_i}\)

　ここで，\(C_i\)は要素iの粘着力，\(ϕ_i\)は内部摩擦角，\(s_i\)はすべり方向を表すベクトルを示しています．

1.2 解析コード

　解析コードは弊社で開発しているPOST-S/3Dを用います．

2. 解析事例の紹介

2.1 解析条件

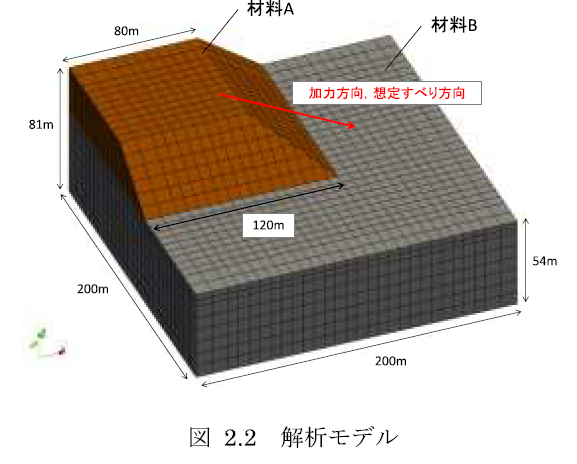
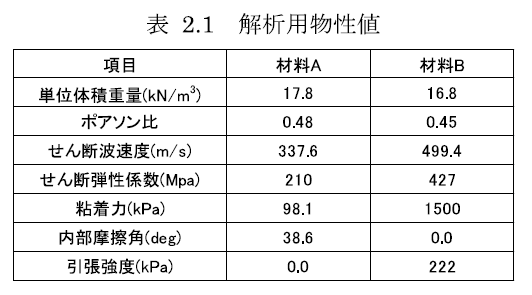
　本文で紹介する評価事例の解析モデルは既往論文²⁾ を参考としています．図 2.2にモデル図を示し，表 2.1に解析用物性値を示します．図 2.2に示している通り，解析モデルは2種類の材料（材料AとB）から構成されています．

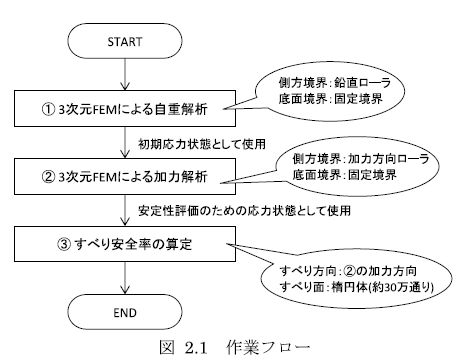
　図 2.1に作業フローを示します．まず，自重解析を行いモデルの常時応力を評価します（①）．この時の側方境界条件は鉛直ローラとし，底面境界条件は固定とします．次に，①で算定された応力を初期状態として，水平方向の震度を0.3¹⁾ とした加力解析を実施します（②）．このときの加力方向はX方向から45°だけ傾けた方向であり，図 2.2にて赤矢印で示した方向です．なお，この時の側方境界条件は加力方向ローラとし，底面境界条件は固定とします．最後に，②で算定された応力状態を用いてすべり安全率の算定を行います（③）．このとき想定するすべり方向は②の加力方向と同一とし，想定するすべり面は楕円体とします．楕円体の形状は，楕円体の中心座標，全体座標系3方向成分の半径をパラメータとする約30万通りのすべり面を設定します．

2.2 解析結果

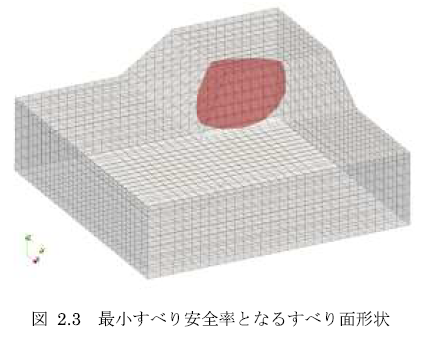
　解析結果として図 2.3に最小すべり安全率となるすべり面形状を示します．このすべり面が解析条件で示した約30万通りのすべり面のうち，最小すべり安全率となるすべり面形状となります．図より，すべり面は凸部を含む形状となっていることが分かります．凸部は他に比べて3次元的な側方拘束効果が期待できないため，すべり安全率が低くなる傾向があります．今回，実施した解析結果は最小すべり安全率となるすべり面が凸部を含んでいることから，この傾向と整合しているといえます．なお，今回の条件では，最小すべり安全率は2.75となりました．原子力分野の場合，周辺斜面の評価基準値は1.2と定められています¹⁾が，これは2次元モデルによる評価基準ですので，そのまま用いることはできません．別途，3次元モデルを用いた場合の基準値が必要となります．

　今回ご紹介した解析事例は水平震度を0.3と設定しましたが，3次元の応力状態は地震動（時刻歴データ）を入力した地震応答解析結果を用いることも可能です．