構造設計等で用いられる設計用入力地震動は、地盤応答解析における地表や基礎下面等における地震動が採用されることが多いと言えます。SHAKEに代表される等価線形化法や、近年では液状化を考慮した有効応力解析なども使われるようになっております。今回は、地震動が鉛直下方から伝播してくる条件の下で、単純な2層地盤を想定して、表層地盤の増幅特性について簡単に紹介したいと思います。また、地盤は小さなひずみ状態でも非線形性を有し減衰効果が見られますが、ここでは減衰効果は考えず地層構造に着目しております。
地震波を地盤内のある地中深度(観測計が設置されている深度など)で観測した場合、その地中の地震波は様々な条件により増幅(もしくは減少)した記録となっております。ここでは、最も簡単な条件(2層地盤による鉛直伝播)で地震波(S波)の特性を見てみます。
地震波は音などと同じ波動ですので、地中内における地層境界で透過や反射が起こります。図1に示すように、下方から入射してくる成分(上昇波:E)と、上方で反射され下降して くる成分(下降波:F)の両方が重なり合った地震波(E+F)として観測されます。
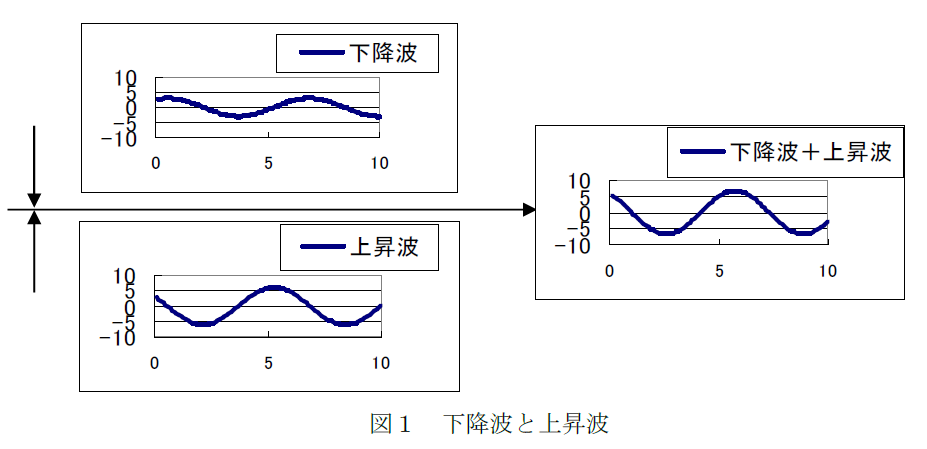
一般に地盤は層構造を成しており、層毎に異なった地盤物性(密度(\(ρ\))、せん断波速度(Vs)等)となっています。図2に示すように、上昇波Aは地盤内の層境界において、その一部は反射され下降波Bに、残りは透過され上昇波Cになって伝播します。
波動伝播の基本方程式を、層境界での変位、せん断力が連続する条件で解くと、上記の反射する成分の比率\(β\)(反射係数)と透過する成分の比率\(γ\)(透過係数)は次式で表すことができます。

ここで、αは層境界の地盤物性により一義的に決まる波動インピーダンス比と称し、\(α=ρ\)2・Vs2/\(ρ\)1・Vs1(上層の密度・速度/下層の密度・速度)で表されます。
地表面(露頭面)では、上層がない(もしくは無視する)ため、\(α\)=0.0となり全反射します。したがって、上昇波=下降波となって伝播するため、地表面での地震波は上昇波の2倍(2Eと呼ばれる)として評価されます。
地震波が基盤に入射した場合の応答振幅比(基盤入射波:2E0に対する地表面の応答:E+F)は、波動インピーダンス比\(α\)で以下のように表せます。この式では減衰効果は無視しています。
\(\left|\frac{E+F}{2E_0}\right| = \frac{1}{\sqrt{cos^2(ωH/V_s)+α^2sin^2(ωH/V_s)}} \)
ここで、ωは角振動数、H、Vsは表層の層厚、せん断波速度を示します。
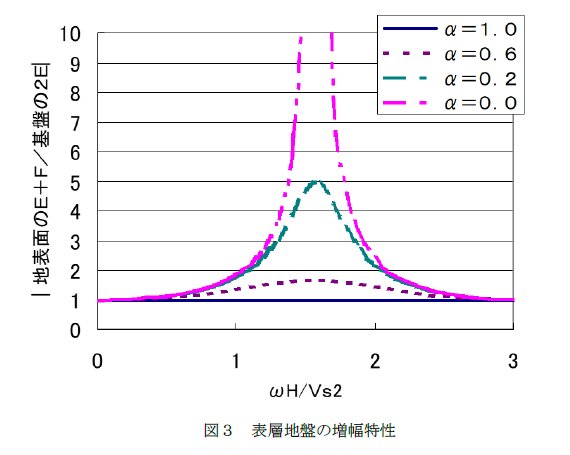
上式及び図3より、\(ω\)H/Vs=(2n-1)\(π\)/2で大きな増幅となることがわかります。\(ω\)H/Vs=\(π\)/2の状態すなわち、f1=Vs/(4H)が、この表層地盤の1次の卓越振動数にあたり、f2=3×Vs/(4H)が2次の卓越振動数にあたります。
まとめ
今回は、地層境界に着目し、インピーダンス比が地震動増幅に影響していることを簡単に紹介いたしました。
比較的小さな地震では、地盤の非線形も小さいためにインピーダンス比により地震動の増幅を検討することが可能ですが、構造物に被害を及ぼすような大きな地震では、地盤の非線形も大きく、インピーダンス比による影響以上に地盤の軟化による剛性低下、さらに減衰効果による影響で地中内の地震動が変動するため、非線形解析等による詳細な検討が必要です。


 (13 投票, 平均: 1.00 / 1)
(13 投票, 平均: 1.00 / 1)