今回は杭の応答変位法計算プログラムk-PILEお問合せ事例として、杭に設定する曲げモーメント-曲率関係(以降、「M-φ関係」と呼ぶこととします)に関する投稿となります。
「M-φ関係の設定はどのように計算すればよいですか。」とご連絡をいただいた場合ですが、基本的に「設計者が決定するものとなり各種指針から計算を行ってください。」という回答となります。具体的には道路橋示方書・同解説(以降、「道示」と呼ぶこととします)や建築基礎構造設計指針などを参照いただき、市販のM-φ関係算定ツールなどをご利用いただくのが一般的かと思います。
一例になりますが、鋼管杭のM-φ関係は、道示IV下部構造編(H29)P298では設計実務の簡素化を考慮したバイリニア型のモデル化が紹介されていますので、以下の(解10.9.1)~(解10.9.9)を用いて勾配変化点となるの全塑性モーメント及び勾配変化点の曲率を計算してみます。
-------------------------------
(解10.9.1) \(M_p = M_{p0}cos(απ/2)\)
(解10.9.2) \(φ'_y = (M_p/M_y)φ_y\)
(解10.9.3) \(M_{p0} = Z_pσ_y\)
(解10.9.4) \(M_y = (σ_y-N/A)Z_e\)
(解10.9.5) \(α = N/N_0\)
(解10.9.6) \(N_0 = σ_yA\)
(解10.9.7) \(Z_p = \frac{4}{3}r^3\left\{(1-(1-t/r)^3\right\}\)
(解10.9.8) \(Z_e = \frac{π}{4}\left\{r^4-(r-t)^4\right\}/r\)
(解10.9.9) \(φ_y = M_y/EI\)
ここに、 \(M_p\):鋼管杭及び鋼管ソイルセメント杭の全塑性モーメント\((kN・m)\) \(φ'_y\):勾配変化点の鋼管杭及び鋼管ソイルセメント杭の曲率\((1/m)\) \(M_{p0}\):軸力がない場合の鋼管杭及びソイルセメント杭の全塑性モーメント\((kN・m)\) \(M_y\):鋼管杭及び鋼管ソイルセメント杭の降伏モーメント\((kN・m)\) \(α\):モーメントがない場合の降伏軸力\(N_0\)と作用軸力\(N\)の比 \(N_0\):モーメントがない場合の降伏軸力\((kN)\) \(Z_p\):鋼管の塑性断面係数\((m^3)\) \(Z_e\):鋼管の断面係数\((m^3)\) \(σ_y\):鋼材の降伏強度の特性値\((kN/m^2)\) \(r\):鋼管の半径\((m)\) \(t\):鋼管の板厚\((m)\) \(A\):鋼管の断面積\((m^2)\) \(σ_y\):鋼管の降伏時曲率\((1/m)\) \(EI\):鋼管の曲げ剛性\((kN・m^2)\)
(引用:道示IV下部構造編 平成29年11月 P298-P299)
-------------------------------
杭は鋼管杭(SKK490)を想定し、諸元は以下とします。
| 記号 | 項目名 | 単位 | 数値 |
| \(σ_y\) | 降伏点 | \(kN/m^2\) | 3.15E+05 |
| \(r\) | 半径 | \(m\) | 5.00E-01 |
| \(t\) | 厚さ | \(m\) | 1.90E-02 |
| \(S\) | 腐食しろ | \(m\) | 0.00E+00 |
| \(A\) | 断面積 | \(m^2\) | 5.86E-02 |
| \(I\) | 断面二次モーメント | \(m^4\) | 7.05E-03 |
| \(Z\) | 断面係数 | \(m^3\) | 1.41E-02 |
| \(E\) | ヤング係数 | \(kN/m^2\) | 2.05E+08 |
上記の前提条件を基に、鋼管杭のM-φ関係を求めると次ページのようになります。(作用軸力に関しては解析等で求めた数値を設定することとなります)
| \(Z_e\) | 鋼管の断面係数 | \(m^3\) | 1.41E-02 |
| \(Z_p\) | 鋼管の塑性断面係数 | \(m^3\) | 1.83E-02 |
| \(N_0\) | モーメントが無い場合の降伏軸力 | \(kN\) | 1.84E+04 |
| \(N\) | 作用軸力 | \(kN\) | 9.00E+03 |
| \(α\) | モーメントが無い場合のN0とNの比 | 4.88E-01 | |
| \(M_y\) | 降伏モーメント | \(kN・m\) | 2.27E+03 |
| \(M_{p0}\) | 軸力がない場合の全塑性モーメント | \(kN・m\) | 5.76E+03 |
| \(φ_y\) | 降伏曲率 | \(1/m\) | 1.57E-03 |
| \(M_p\) | 全塑性モーメント | \(kN・m\) | 4.15E+03 |
| \(φ'_y\) | 勾配変化点の曲率 | \(1/m\) | 2.87E-03 |
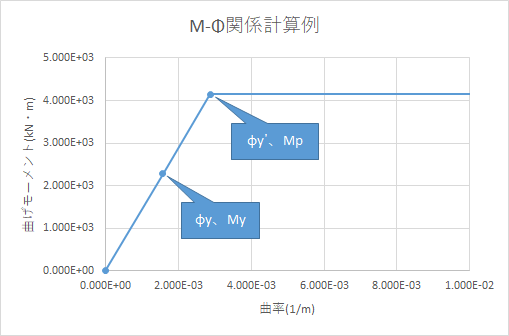
k-PILEでは今回求めた折れ点を入力することにより、バイリニア型の杭非線形特性を設定することができます。なお、バイリニア以外にトリリニア、4折れ線まで設定が可能となっています。


 (2 投票, 平均: 1.00 / 1)
(2 投票, 平均: 1.00 / 1)