DEM(個別要素法)とは?
DEM(個別要素法) は、Cundall[1971]によって提案された数値解析手法です。当初は岩石ブロックの接触と運動を解くブロックに対してDEMが用いられましたが、現在は主に粉体のような粒子の集合体を取り扱うためにDEMが使われています。球形粒子などを用いた粒子ベースの計算(球形粒子や円筒形粒子)では、ブロックベースの計算に比べて接触判定が容易であるため、多数の粒子を取り扱うことができます。
DEMは接触や剛体回転を取り扱うことができるため、大変形問題を得意としており、土木建築分野では斜面崩壊や土石流などの地盤の挙動解析や、石垣の挙動解析などに適用されています。
解析手法
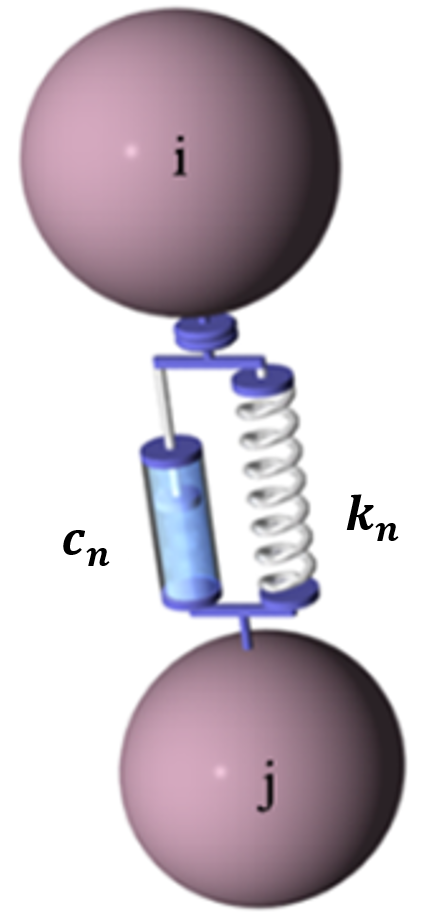
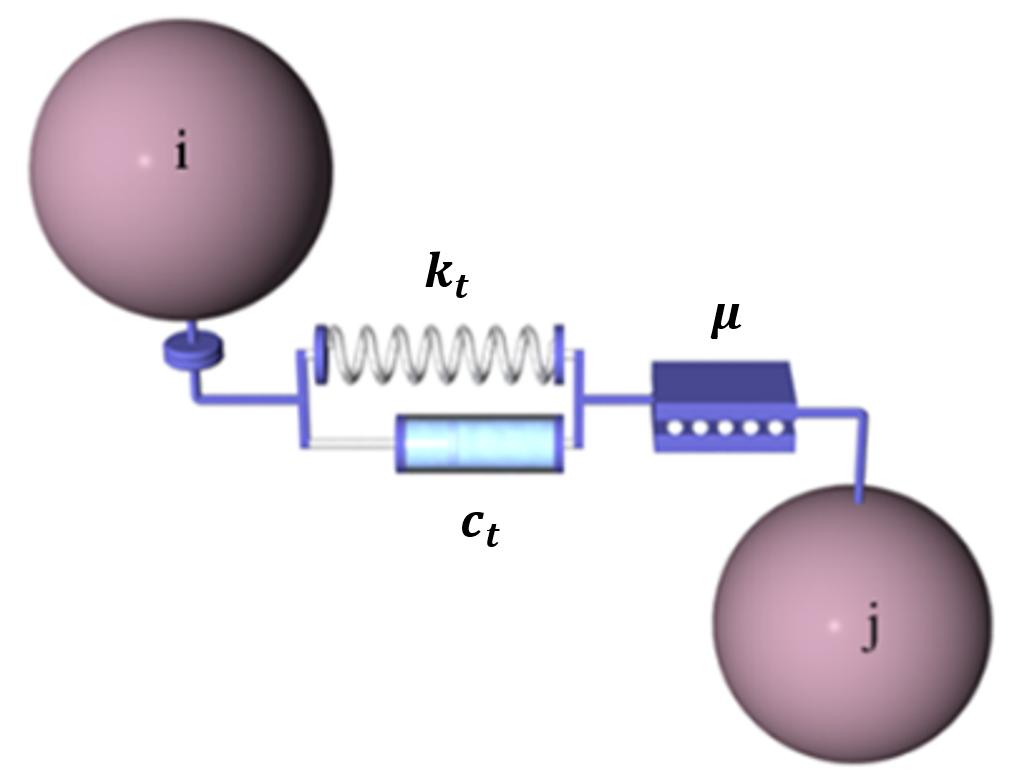
球形粒子を用いたDEMの解析手法では、粉体や粒状体を変形しない粒子(剛体粒子)の集合体で模擬します。 ただし、完全な剛体を仮定すると多体接触を取り扱うことができないため、剛体粒子にオーバーラップを許容します。粒子間に働く接触力を法線方向と接線方向に分解し、各方向の力をばねとダッシュポットとスライダーで模擬したモデル (下図参照) が一般的に採用されています。
 |  |
| (a)法線方向 | (b)接線方向 |
ばね定数 (\(k_n\)、 \(k_t\) )は衝突時間に影響し、ばね定数が大きい程衝突時の接触時間が短くなります。粘性減衰係数 \(c_n\)、 \(c_t\) は反発力を表し、粘性減衰係数が大きい程跳ね返り係数が小さくなります。スライダー \(\mu\)は粒子間の摩擦の大きさを表しており、安息角などに影響します。
近傍粒子探索アルゴリズムについて
DEMのプログラミングにおける高速化の方法として、近傍粒子探索アルゴリズムがあります。 近傍粒子探索アルゴリズムには様々な方法がありますが、代表的な方法について説明します。
すべての粒子間について接触判定を行おうとすると、粒子数\(N\)の時全粒子の組み合わせが\(N(N-1)/2\)になるため、計算時間は O( \(N^2\))に比例します。そこで、対象粒子の周辺だけで接触判定をすることで計算回数を減らすことを考えます。
まず、計算領域を均一な格子に分割します。格子サイズは粒子直径の最大値(粒子径分布がある場合)よりも大きくします。粒子はその中心座標を含む格子に登録されます。そして、自身の属する格子内の粒子と、隣接する格子内の粒子において接触判定を行います。このようにすれば、計算時間が O( \(N\) ) に比例するように削減できます。
ただし、上記の方法をプログラムに実装する際に、メモリ消費量が増加し、粒子数多い大規模な体系でメモリ不足になる問題があります。各格子に一定の大きさの配列を確保するため、粒子がほとんど属さない格子にもメモリ容量を確保しており、メモリを無駄遣いしています。そこでリンクリスト(連結リスト)を用いたアルゴリズムを用います。
このアルゴリズムでは、各格子で共有する大きさ\(N\)(粒子数)の配列next[粒子番号](リンクリスト用配列)と、格子内で一番若い粒子番号を表す配列cellFirst[格子番号]を用います。例えば、ある格子に粒子番号i, j ,k(i<j<k) の粒子が存在する場合は、 cellFirst[格子番号]=i ⇒ next[i]=j ⇒ next[j]=k ⇒ next[k]=-1のようにして、格子に存在する粒子i、j、kが得られます。リンクリストを用いることで、配列の大きさは \(N\) 以下に抑えられるため、メモリ消費量を大幅に削減できます。
DEMのプログラムの流れ
DEMのプログラムの流れについて説明します。(下記フローチャートを参照)
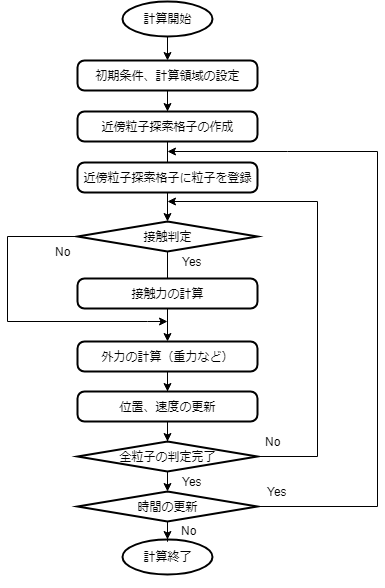
プログラム開始時に初期条件や計算領域を決定します。次に、近傍粒子探索アルゴリズムで計算領域を格子に分割し、各格子に粒子を登録します。
1番目の粒子において近傍の粒子や境界との接触判定を行い、接触していれば接触力を計算します。接触力の他、外力(重力など)を加算します。粒子に働く力を求めたら、位置、速度を求めます。この際、オイラー法や蛙飛び法などの時間差分の積分手法が用いられます。(今回は時間差分の積分手法についての説明は割愛します。)
上記の接触判定から位置、速度を求める手順を2番目以降の粒子について行います。全ての粒子について手順が完了したら、時刻を更新し、近傍粒子探索格子に再度粒子を登録した後、1番目の粒子から手順を繰り返します。以上を最終時刻まで繰り返すと計算終了になります。
まとめ
今回は、DEMの基本的な解析手法( 接触点のモデル化や近傍粒子探索法など )について説明しました。
次回「DEM解析その(2)」では、DEM解析におけるパラメータについて説明する予定です。
参考文献
- 酒井幹夫 『粉体の数値シミュレーション』 丸善出版、2012年


 (4 投票, 平均: 1.00 / 1)
(4 投票, 平均: 1.00 / 1)