プラント施設等においては、燃料への引火による爆発事故が発生するリスクがある。爆発発生時に生じる風圧は爆風圧と呼ばれ、正圧と負圧からなるパルス状の時刻歴性状を有していることが知られている。構造物の耐爆設計においては、爆風圧の正圧部分のみを三角波で置換する手法が多く用いられる1)ものの、負圧が構造物の応答に与える影響が無視できない場合も考えられる。本資料では正圧と負圧を有する爆風圧に対する構造物の応答を理論的に導出することを試みるものである。
質量m、固有円振動数ωの1自由度系に対し、図1で示すような時刻歴荷重が作用する場合、任意の時刻tにおける変位応答uは以下の畳み込み積分により評価される。
\(u=\int_0^t\frac{P(t)}{\omega m}\sin\omega(t-\tau)d\tau\)
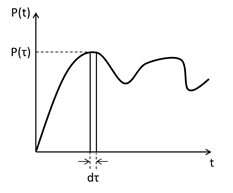
図1 任意の時刻歴荷重
ここで、評価対象とする爆風圧時刻歴を図2のように定義する。以降では、図2の爆風圧時刻歴荷重に対する1自由度系の応答を、上に示した畳み込み積分を用いて算出していく。
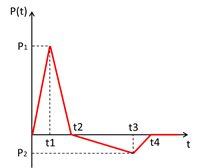
図2 正圧・負圧を有する三角波時刻歴
図2の荷重時刻歴は時刻tに応じて、以下の式で表現することができる。
\begin{eqnarray} P(t)=\left\{\begin{array}{lllll} \frac{P_1}{t_1}t (0\le t\le t_1)\\ \frac{-P_1}{t_2-t_1}(t-t_2) (t_1< t\le t_2)\\ \frac{P_2}{t_3-t_2}(t-t_2) (t_2< t\le t_3)\\ \frac{-P_2}{t_4-t_3}(t-t_4) (t_3< t\le t_4)\\ 0 (t_4<t)\end{array}\right.\end{eqnarray}
したがって、任意の時刻tにおける変位uは、上記のP(t)それぞれに対して畳み込み積分を適用することで評価が可能である。以下がその計算結果である。
1) \(0\leq t\leq t_1\)
\(u=\int_0^t \frac{P(\tau)}{\omega m}\sin\omega(t-\tau)d\tau=\int_0^t \frac{P_1}{\omega mt_1}\tau\sin\omega(t-\tau)d\tau\)
2) \(t_1< t\leq t_2\)
\(u=\int_0^t \frac{P(\tau)}{\omega m}\sin\omega(t-\tau)d\tau\)
\(=\int_0^{t_1} \frac{P_1}{\omega mt_1}\tau\sin\omega(t-\tau)d\tau+\int_{t_1}^t \frac{-P_1}{\omega m(t_2-t_1)}(\tau-t_2)\sin\omega(t-\tau)d\tau\)
\(=\frac{P_1}{\omega^2 mt_1}\left\{t_1\cos\omega(t-t_1)+\frac{\sin\omega(t-t1)}{\omega}-\frac{\sin\omega t}{\omega}\right\}+\frac{P_1}{\omega^2m(t_2-t_1)}\\\left[t_2\left\{1-\cos\omega(t-t_1)\right\}-\left\{t-t_1\cos\omega(t-t_1)-\frac{\sin\omega(t-t_1)}{\omega} \right\}\right]\)
3) \(t_2< t\leq t_3\)
\(u=\int_0^t \frac{P(\tau)}{\omega m}\sin\omega(t-\tau)d\tau\\=\int_0^{t_1} \frac{P_1}{\omega mt_1}\tau\sin\omega(t-\tau)d\tau+\int_{t_1}^{t_2} \frac{-P_1}{\omega m(t_2-t_1)}(\tau-t_2)\sin\omega(t-\tau)d\tau\\+\int_{t_2}^t \frac{P_2}{\omega m(t_3-t_2)}(\tau-t_2)\sin\omega(t-\tau)d\tau\)
\(=\frac{P_1}{\omega^2 mt_1}\left\{t_1\cos\omega(t-t_1)+\frac{\sin\omega(t-t_1)}{\omega}-\frac{\sin\omega t}{\omega}\right\}+\frac{P_1}{\omega^2m(t_2-t_1)}\\\left[t_2\left\{\cos\omega(t_2-t_1)-\cos\omega(t-t_1)\right\}-\left\{t_2\cos\omega(t-t_2)-t_1\cos\omega(t-t_1)\\+\frac{\sin\omega(t-t_2)}{\omega}-\frac{\sin\omega(t-t_1)}{\omega} \right\}\right]\\+\frac{P_2}{\omega^2m(t_3-t_2)}\left[t-t_2\cos\omega(t-t_2)-\frac{\sin\omega(t-t_2)}{\omega}-t_2\left\{1-\cos\omega(t-t_2)\right\}\right]\)
4) \(t_3< t\leq t_4\)
\(u=\int_0^t \frac{P(\tau)}{\omega m}\sin\omega(t-\tau)d\tau\)
\(=\int_0^{t_1} \frac{P_1}{\omega mt_1}\tau\sin\omega(t-\tau)d\tau+\int_{t_1}^{t_2} \frac{-P_1}{\omega m(t_2-t_1)}(\tau-t_2)\sin\omega(t-\tau)d\tau\)
\(+\int_{t_2}^{t_3} \frac{P_2}{\omega m(t_3-t_2)}(\tau-t_2)\sin\omega(t-\tau)d\tau+\int_{t_3}^t \frac{-P_2}{\omega m(t_4-t_3)}(\tau-t_4)\sin\omega(t-\tau)d\tau\)
\(=\frac{P_1}{\omega^2 mt_1}\left\{t_1\cos\omega(t-t_1)+\frac{\sin\omega(t-t_1)}{\omega}-\frac{\sin\omega t}{\omega}\right\}+\frac{P_1}{\omega^2m(t_2-t_1)}\\\left[t_2\left\{\cos\omega(t_2-t_1)-\cos\omega(t-t_1)\right\}-\left\{t_2\cos\omega(t-t_2)-t_1\cos\omega(t-t_1)\\+\frac{\sin\omega(t-t_2)}{\omega}-\frac{\sin\omega(t-t_1)}{\omega} \right\}\right]+\frac{P_2}{\omega^2m(t_3-t_2)}\\\left[t_3\cos\omega(t-t_3)-t_2\cos\omega(t-t_2)+\frac{\sin\omega(t-t_3)}{\omega}-\frac{\sin\omega(t-t_2)}{\omega}\\-t_2\left\{\cos\omega(t-t_3)-\cos\omega(t-t_2)\right\}\right]+\frac{P_2}{\omega^2m(t_4-t_3)}\\\left[t_4\left\{1-\cos\omega(t-t_3)\right\}-\left\{t-t_3\cos\omega(t-t_3)-\frac{\sin\omega(t-t_3)}{\omega}\right\}\right]\)
5) \(t_4< t\)
\(u=\int_0^t \frac{P(\tau)}{\omega m}\sin\omega(t-\tau)d\tau\)
\(=\int_0^{t_1} \frac{P_1}{\omega mt_1}\tau\sin\omega(t-\tau)d\tau+\int_{t_1}^{t_2} \frac{-P_1}{\omega m(t_2-t_1)}(\tau-t_2)\sin\omega(t-\tau)d\tau\)
\(+\int_{t_2}^{t_3} \frac{P_2}{\omega m(t_3-t_2)}(\tau-t_2)\sin\omega(t-\tau)d\tau+\int_{t_3}^{t_4} \frac{-P_2}{\omega m(t_4-t_3)}(\tau-t_4)\sin\omega(t-\tau)d\tau\)
\(=\frac{P_1}{\omega^2 mt_1}\left\{t_1\cos\omega(t-t_1)+\frac{\sin\omega(t-t_1)}{\omega}-\frac{\sin\omega t}{\omega}\right\}+\frac{P_1}{\omega^2m(t_2-t_1)}\\\left[t_2\left\{\cos\omega(t_2-t_1)-\cos\omega(t-t_1)\right\}-\left\{t_2\cos\omega(t-t_2)-t_1\cos\omega(t-t_1)\\+\frac{\sin\omega(t-t_2)}{\omega}-\frac{\sin\omega(t-t_1)}{\omega} \right\}\right]+\frac{P_2}{\omega^2m(t_3-t_2)}\\\left[t_3\cos\omega(t-t_3)-t_2\cos\omega(t-t_2)+\frac{\sin\omega(t-t_3)}{\omega}-\frac{\sin\omega(t-t_2)}{\omega}\\-t_2\left\{\cos\omega(t-t_3)-\cos\omega(t-t_2)\right\}\right]+\frac{P_2}{\omega^2m(t_4-t_3)}\\\left[t_4\left\{\cos\omega(t-t_4)-\cos\omega(t-t_3)\right\}-\left\{t_4\cos\omega(t-t_4)-t_3\cos\omega(t-t_3)\\+\frac{\sin\omega(t-t_4)}{\omega}-\frac{\sin\omega(t-t_3)}{\omega} \right\}\right]\)
1)例えば、基礎からの爆発安全工学 -構造物の耐爆設計の基礎 大野友則 森北出版
構造計画研究所では耐衝撃・耐爆解析およびそのコンサルティングを実施しております。
https://www4.kke.co.jp/kaiseki/service/disaster/dis_13.html


 (4 投票, 平均: 1.00 / 1)
(4 投票, 平均: 1.00 / 1)