1.はじめに
構造物の耐震性能を向上させるための大きな考え方として、耐震、制振、免震の3つが知られている。それぞれの言葉の意味するところは次の通りである。
耐震:地震力に抵抗するため、斜材の挿入などにより構造物自体の剛性を向上させる
制振:構造物に発生した応答を、ダンパーなどを用いて減衰させる
免震:地震動の周期成分から構造物の振動周期を外すことを目的に、構造物基部にゴム等を設置し固有周期を変化させる。
耐震における斜材の挿入とは、図1のようなイメージである。図の左の状態ではフレーム自体の剛性で外力に抵抗しなければならないが、右の状態ではフレームの剛性に加え斜材の剛性を外力に対する抵抗力に見込むことが可能となる。
ここでは、斜材の挿入前後でフレーム構造の剛性がどれだけ向上するかを理論的に求めていくこととする。
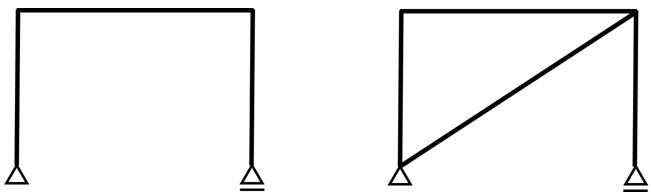
図1 フレーム構造への斜材の挿入
2.問題の定義
対象とするフレーム構造は図1に示したものとする。ただし、簡単のため挿入する斜材はトラス材とし、一次不静定構造として取り扱うこととする。図2には荷重条件や対象とする構造物の断面諸元・寸法を示す。なお、ここで扱う問題は全て線形弾性範囲内、梁のせん断変形は考慮しないものとする。
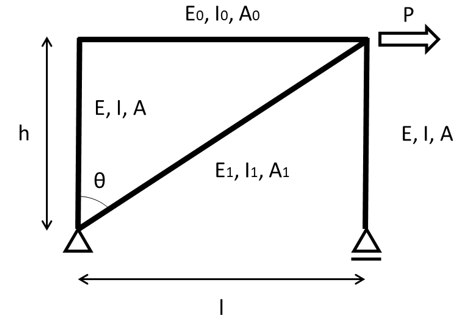
図2 対象構造物と断面諸元、荷重条件
3.変形状態の幾何学的関係
水平荷重を受けたフレーム構造は、概ね図3のような変形形状となる。以降の変形図では変形状態をやや誇張して表現しているが、実際にはフレームの接合部は直角を保っている。ここで、微小変形を仮定し、斜材の変形量をδTとすると、δT、δx、δy、h、lの間には以下の関係が成立する。
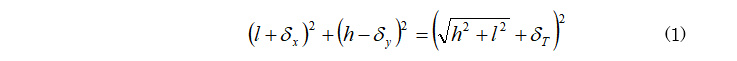
左辺第一項は左側の支点から斜材上端までの水平距離、左辺第二項は斜材上端の鉛直変位量、右辺は変形後の斜材長である。
なお、斜材軸力をT(未知量)とするとδTは
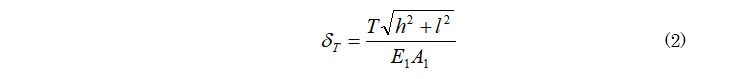
と表記できる。
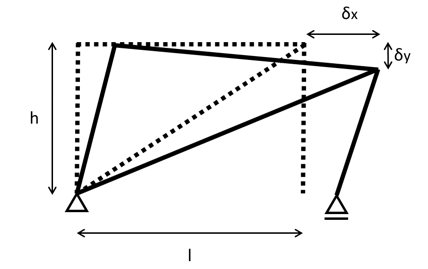
図3 構造物の変形状態
4.仮想仕事の原理による求解
一次不静定問題を仮想仕事の原理を用いて解く場合、「0系」、「1系」と呼ばれる静定構造問題に分解して諸量を算出していくことが一般的である。以下に、図2の問題へこれを適用した場合について示す。
まず、一次不静定構造である図2の構造を、斜材を取り除くことで静定構造とする。まず「0系」であるが、これは斜材を除いたフレーム構造に水平荷重を作用させる問題として定義する。次に「1系」であるが、これは斜材が存在することにより「0系」に比べどれだけ変形が抑制されるかを表す力学系となる。したがって、斜材軸力Tに相当する力を作用させた図5のような問題としてとらえることができる。
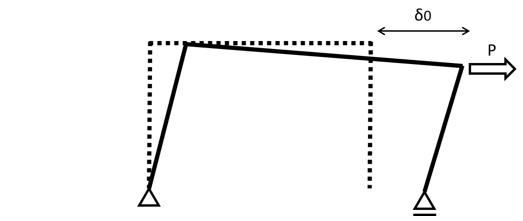
図4 「0系」における変形状態
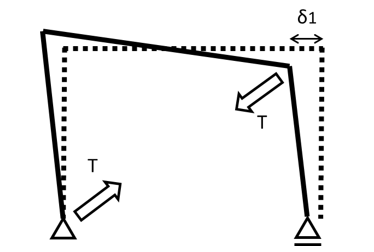
図5 「1系」における変形状態
それぞれの系における変位δ0、δ1は静定構造であることから容易に求めることができ、図2、図3の諸元を用いて以下のように表すことができる。
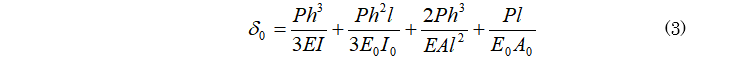
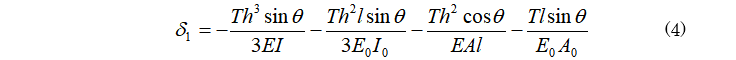
「0系」、「1系」を足し合わせた結果が図3の状態になるわけであるから、以下の関係が成り立つことが分かる。
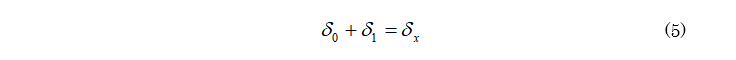
したがって、(5)式に(1)~(4)式を代入することで軸力Tを求めることができる。少し煩雑な計算となるが、最終的にはTの二次方程式に帰着するのでこれを注意深く解いていくことで、
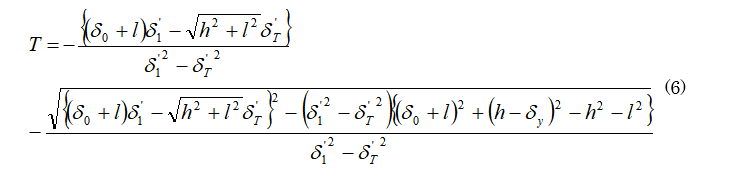
ただし、
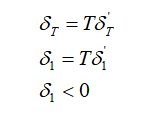
が導かれる。
ここまでの導出において、δyの評価がまだであったので言及しておく。実は図3の構造においては、δyは斜材の有無によらず一定の値をとることを「0系」「1系」の議論から導くことができ、その値は
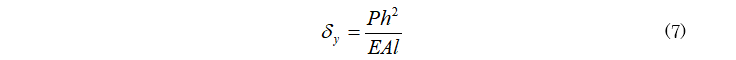
となる。
水平方向のフレーム剛性がどれだけ向上したかは、 δ0 /δx を計算することにより評価することができる。それぞれの式の詳細は上記の導出過程を辿ることで算出が可能であるが、かなり煩雑な式となるためここでは割愛する。
5.数値解析との比較
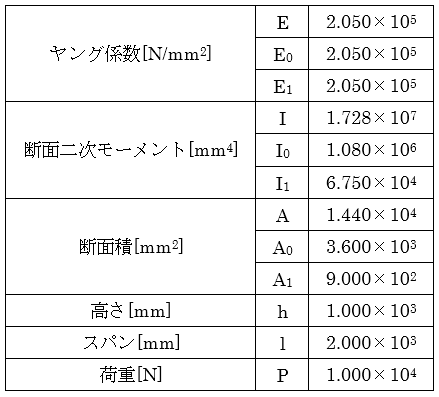
前章で導出した理論解の妥当性を確認するために、汎用ソフトウェア「Midas」の計算結果との比較を行う。解析条件は以下の通りである。
表1 解析諸元
理論解による軸力Tおよび変位δx、δyは以下の値となる。
T = 1.113×104 [N]
δx = 1.5161×10-1 [mm]
δy = 1.6938×10-3 [mm]
Midasによる解析結果を図6~図9に示す。変形状態が分かるよう、変形図は適宜倍率をかけて表示している。これらの図より、数値解析による軸力Tおよび変位δx、δyは以下の値となる。
T = 11126.1 [N]
δx = 0.15161 [mm]
δy = 0.0016938 [mm]
以上の比較から、理論解と数値解析の結果が一致することを確認した。
なお、本条件におけるδ0の値は
δ0 = 31.081 [mm]
である。したがって、斜材1本の挿入により水平方向の剛性は約200倍向上したことになる。

図6 斜材の軸力
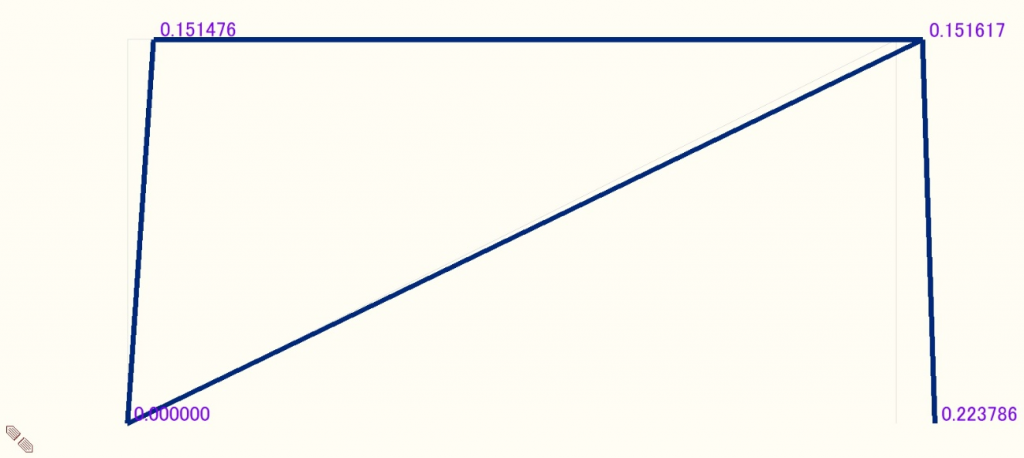
図7 フレーム全体の変形図
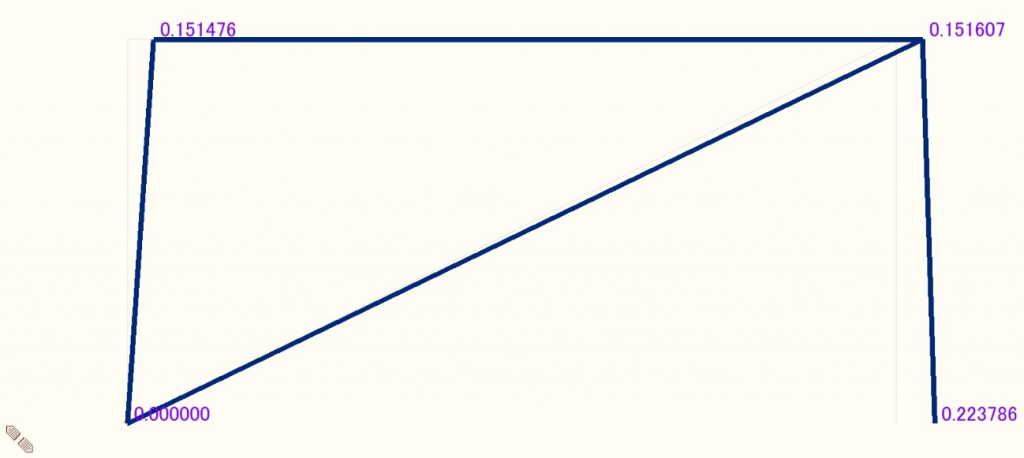
図8 フレームの水平方向変形図
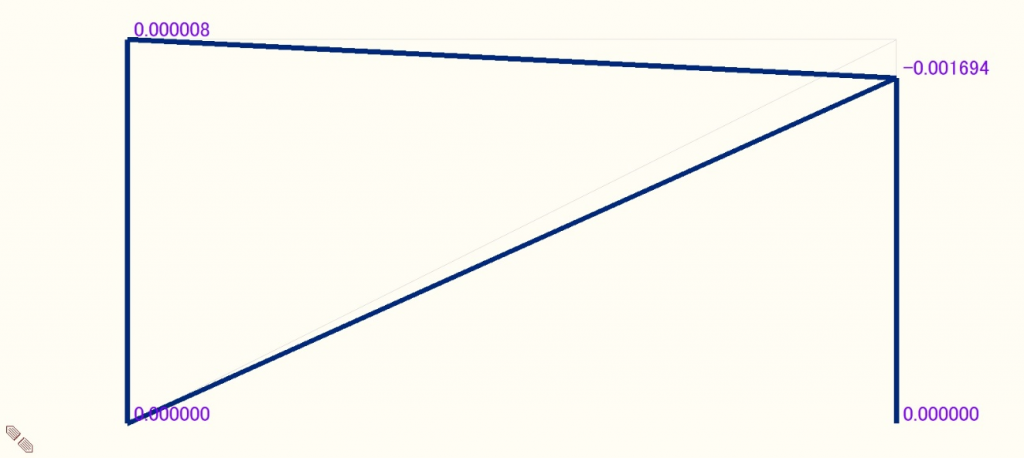
図9 フレームの鉛直方向変形図
6.斜材剛性が変化した時の応答に関する考察
4章で導出した理論解が数値解析の結果と一致したことから、理論解の妥当性が示された。次に、斜材剛性が変化した場合における軸力Tの挙動や、それに伴い変化するであろうδxの動きについて考察を行う。斜材剛性の変化とはE1A1が変化することと同義であるから、ここではE1A1 →0およびE1A1→∞を仮定した評価を行う。 軸力Tは(6)式で評価されるが、(6)式においてE1A1の関数となっているのは σ'Tである。
まず、E1A1 →0のとき、![]() であるから(6)式は以下のように評価される。
であるから(6)式は以下のように評価される。
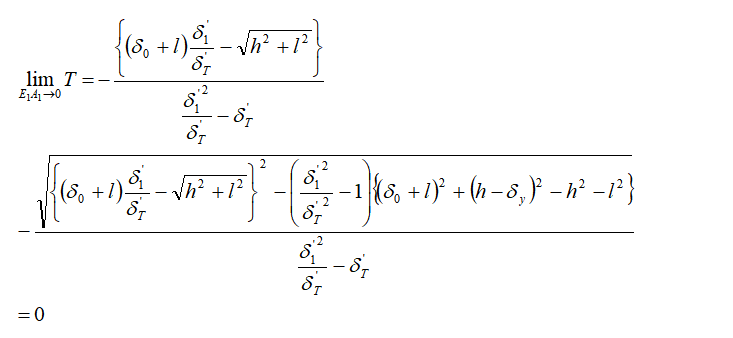
このとき、(5)式の第2項が0となることから、
δx= δ0
と求められる。これは自明なことではあるが、斜材がない状態に相当する。
次に、E1A1→∞とした場合、![]() であるから (6)式は以下のように評価される。
であるから (6)式は以下のように評価される。
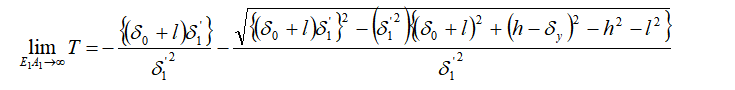
すなわち、斜材を剛体に近づけた場合、発生する軸力が一定値に漸近することとなる。ただし、![]() であることから斜材には当然変形は発生せず、したがって(1)式より
であることから斜材には当然変形は発生せず、したがって(1)式より
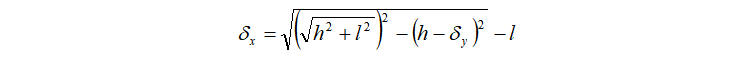
と求められる。これは荷重作用点が斜材端部を回転軸として鉛直方向にδyだけ変位するように回転した状態を表している。
7.まとめ
フレーム構造に斜材を挿入した場合の軸力および変位について、構造力学をもとに理論解を導出した。この理論解と汎用ソフトウェアの解析結果を比較することにより、理論解が正しいことを示した。また、導出した理論解をもとに、パラメータが変化した場合の物理的な意味を考察し、それが力学的なイメージと整合することを確認した。
8.参考:仮想仕事の原理による変位の導出
図4「0系」における、M図およびN図は以下のようになる。
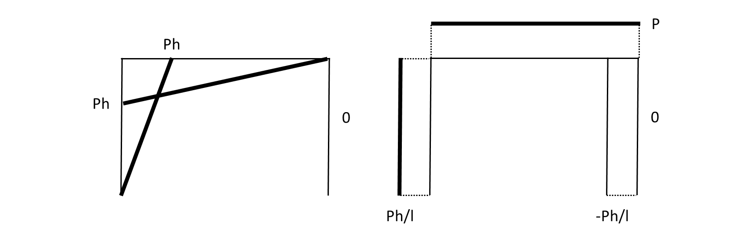
図10 「0系」におけるM図およびN図(左:M図、右:N図)
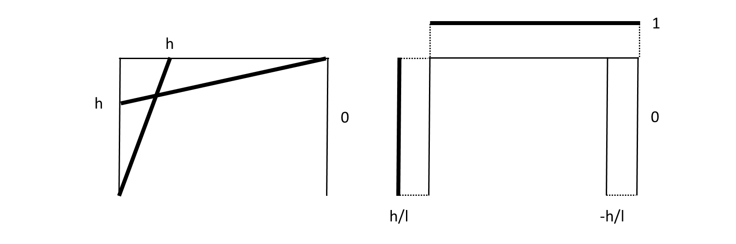
図11 「0_1系」におけるM図およびN図(左:M図、右:N図)
仮想仕事の原理では、エネルギーのつり合いの概念に基づき以下の関係が成立する。
(仮想外力)×(実変位)=(仮想内力)×(実変形)
今回の「0系」および「0_1系」では、それぞれの項は以下のように定義される。
(仮想外力)= 1
(実変位)= δ0 ・・・未知量
(仮想内力)= 「0_1系」におけるモーメントおよび軸力
(実変形)= 「0系」におけるひずみ
ここで実変形、すなわち「0系」におけるひずみは発生断面力を部材剛性で除すことで算出することができる。したがって、「0_1系」におけるモーメントと軸力をそれぞれM、N とおくと、
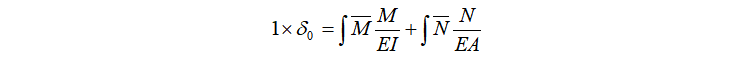
という関係式が導かれる。ここでの積分変数は部材の長さであるから、図10、図11の断面力を関数として上式に代入すると、δ0を算出することができる。
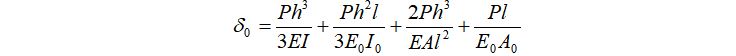
なお、δ1については、「1系」における各部材の断面力を用いて実変形を定式化することで導出できる。


 (7 投票, 平均: 1.00 / 1)
(7 投票, 平均: 1.00 / 1)