地震が起こると、いろいろな物が倒れたり落下したりします。部屋の中は当然ぐちゃぐちゃになり、人が怪我をしたり、最悪の場合亡くなってしまうこともあります。 このような被害に対する対策を考えていく上で、どれくらいの揺れの大きさで物が倒れるのか、どのくらいの被害になるのかを予測しておくことが重要です。
今回の記事では、「 どれくらいの揺れの大きさで物が倒れるのか 」について、国や自治体の地震被害想定や企業のBCP(事業継続計画)策定時によく用いられている評価方法をご紹介します。
震度と物の動きの関係
揺れの大きさの指標として様々なものがありますが、その中でも震度は一番なじみ深く、揺れの大きさをイメージしやすいと思います。最初に、震度と物の動きの関係についてお話しします。
過去の文献(岡田・鏡味, 1991)によると、 震度と物の動きの関係は下図のようになっています。横軸が震度で縦軸が被害率を表しています。「ロッキング」とは物がカタカタと傾きながら揺れる挙動です。この図によると、「軽いまたは背の高い家具の転倒」は震度5弱から発生し始め、震度6強になると被害率は70%以上になり、ほとんどの「 軽いまたは背の高い家具 」が転倒してしまうことが分かります。
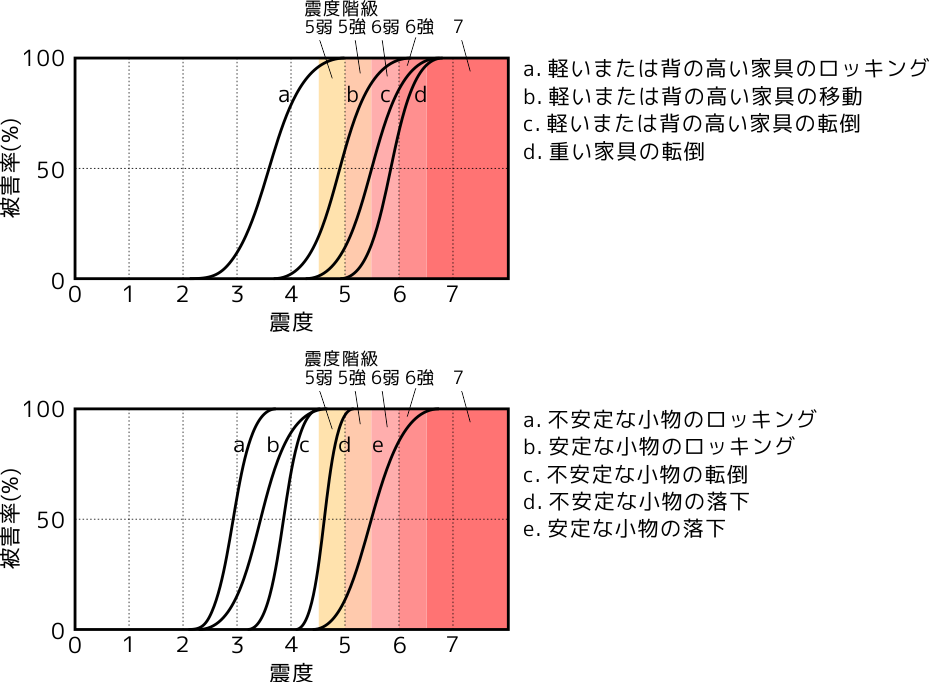
揺れの加速度と物の動きの関係
震度は揺れの大きさがイメージしやすいのがいいところですが、揺れの大きさを厳密に表現できません。そのため、定量的に物の倒れやすさを評価しやすいように、揺れの大きさの指標として最大加速度や最大速度をよく用います。
ここからは、企業のBCP策定時等によく用いられている最大加速度や速度と物の動きの関係式をご紹介していきます。
物の動きの予測方法
書籍「長周期地震動と超高層建物の対応策 -専門家として知っておきたいこと- 日本建築学会」に掲載されている物の動きの予測方法を以下に示します。本棚等の物を矩形の剛体だと仮定し、その幅高さ比・摩擦係数、床の揺れの大きさ・卓越周期を用いて、地震時の動きを予測します。
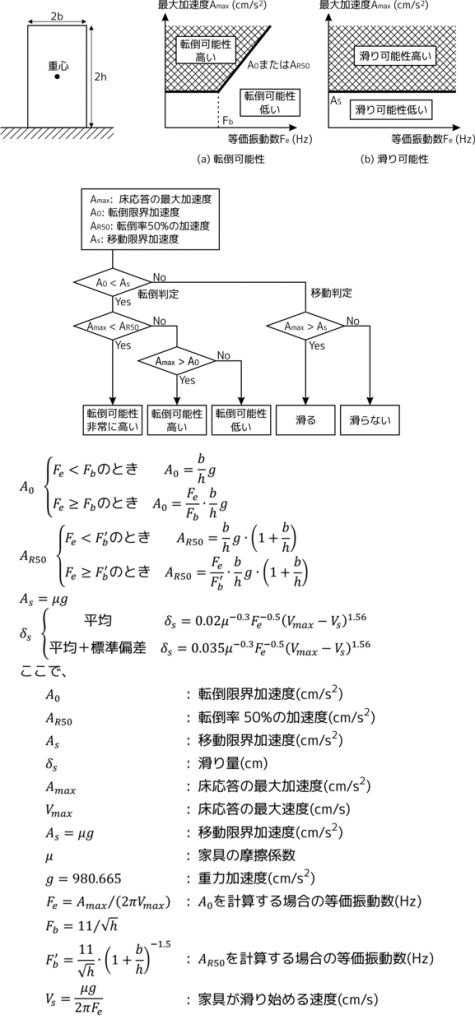
書籍「長周期地震動と超高層建物の対応策 -専門家として知っておきたいこと- 日本建築学会」 を元に作成
上記方法に従って計算される転倒限界曲線は以下のようになります。右側のオレンジの曲線が転倒限界加速度(転倒し始める加速度)を表しており、曲線よりも上の領域だと転倒可能性が高く、下だと転倒可能性が低いという判定となります。図の横軸は揺れの卓越周期で、主に想定地震波の卓越振動数や建物の共振振動数を考慮して設定します。
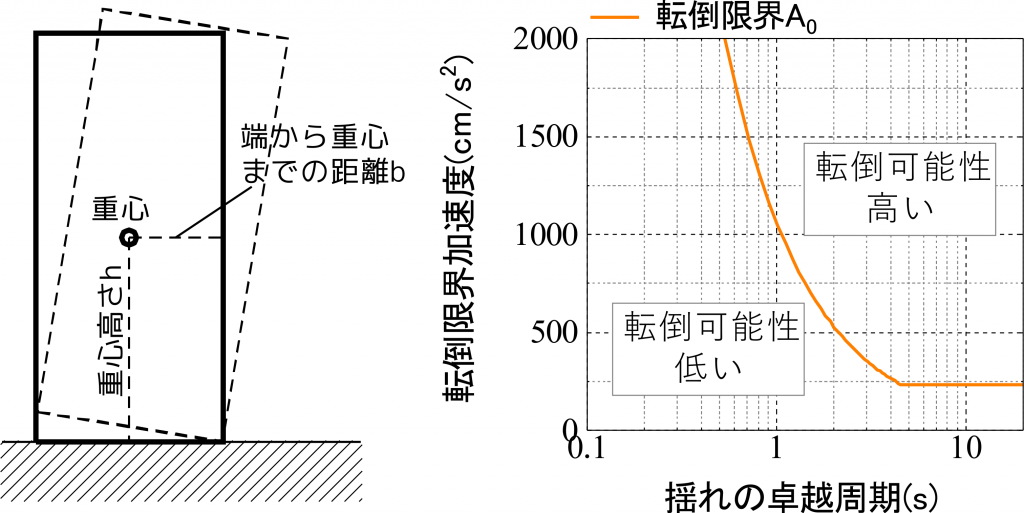
この手法は、非常に少ない情報だけで物の動きが予測できて実用的なので、様々な場面で用いられています。 しかし、以下のような制限があるので注意が必要です。
- 物が単独で床置きされている状況を想定しており、壁際や背中合わせで配置されていたり、2段以上積み上げられている場合の評価は出来ない。
- 外形が矩形でないものの評価は出来ない。また、変形するようなものの評価は出来ない。
- 周囲の壁や物にぶつかる影響は考慮できない。
なお、このような制限により上記の方法では評価できない物や状況を想定する場合は、以下のような物理シミュレーションを用いて評価する方法もあります。
物の動きの予測例
この関係式を使って実際に本棚とタンスに対して転倒するかどうか評価した結果を以下に示します。この例だと、タンスは地震A・Bに対して転倒可能性が低い結果ですが、本棚については転倒し始めるかどうかの境界線上にいることが分かります。
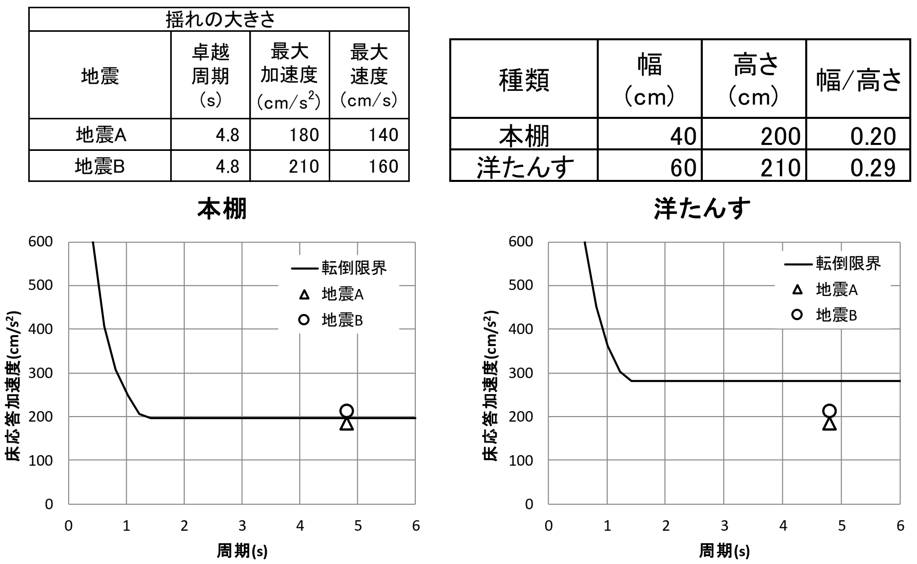
まとめ
本記事では、地震による室内被害対策を考える上で重要な揺れの大きさと物の動きの関係について、よく用いられている評価方法をご紹介しました。


 (1 投票, 平均: 1.00 / 1)
(1 投票, 平均: 1.00 / 1)