RCの劣化予測シミュレーションに向けた拡散解析

はじめに

コンクリートの劣化要因の1つに塩害があります。塩害はコンクリート内部の塩化物イオンにより鉄筋が腐食・膨張しコンクリートにひび割れが生じる現象です。これはコンクリート内部における塩化物イオンの拡散現象と鉄筋が膨張しコンクリートにひび割れが発生する力学現象が組み合わさった現象です。

本記事は、塩害の劣化予測シミュレーションに向けた基礎解析として行った拡散解析についての記事です。

拡散方程式と熱伝導方程式

拡散というと空気中や水中に物質が広がっていくイメージを持たれることが多いと思いますが、コンクリート内部の塩化物イオンはコンクリート細孔内に含まれる水分や湿分中を移動するため、コンクリート内の塩化物イオンの拡散も液体中の拡散と同じように考えられます。

物質が拡散するとき、流束\(J\)（単位時間に単位面積を移動する物質量）は濃度\(c\)の勾配に比例するとされています。この法則をフィックの第1法則と呼び、\(x\)方向への物質の拡散を式で表すと以下のようになります。比例係数である\(D\)は拡散係数と呼ばれ、[面積]/[時間]の次元を持ちます。

\(J=-D\frac{∂c}{∂x}\)

次に、図に示すような\(x～x+Δx\)の領域について考えます。

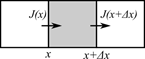
単位時間、単位面積当たりに領域内に流入する物質の量は\(J(x)-J(x+Δx)\)で表されます。また、これは単位時間当たりの濃度変化量でもあります。

\(\frac{∂c}{∂t}△x=J(x)-J(x+△x)\)

式を変形すると、濃度変化と流束変化の関係式が得られます。

\(\frac{∂c}{∂t}=-\frac{∂J}{∂x}\)

\(D\)は\(x\)方向に一定であるとすると、フィックの第1法則から以下の式が得られます。

\(\frac{∂c}{∂t}=D\frac{∂^2c}{∂x^2}\)

これはフィックの第2法則もしくは拡散方程式と呼ばれます。

ここで少し話は変わりますが、熱伝導方程式と拡散方程式について見てみましょう。

元々、拡散の基本法則であるフィックの法則は熱伝導に関するフーリエの法則と同じように考えることができるとして与えられたものです。フーリエの法則では「熱流束は温度勾配に比例する」と考えられていて、熱伝導方程式は\(p\)：比熱、\(c\)：密度、\(q\)：熱流束、\( λ\)：熱伝導係数、\(t\)：温度として以下の式で与えられます。

\(pc\frac{∂T}{∂t}=λ\frac{∂^2T}{∂x^2}\)

熱伝導方程式と拡散方程式を見比べると同じ形をしていることが分かります。つまり、物理量を読み替えることでそれぞれを入れ替えることが可能ということです。

非定常拡散解析の例

熱伝導解析プログラム「ADINA Thermal」（ADINA R&D, Inc.）を用いて2次元の非定常拡散解析を行ってみました。

本解析ではコンクリート表面からコンクリート内部に塩化物イオンが拡散する様子を模擬する解析を行いました。

解析モデルは鉄筋1本を含むコンクリートを模擬し、図の下側から塩化物イオンがコンクリート内に拡散する様子を解析しました。緑色で示す鉄筋はコンクリートのような多孔質材料ではないので塩化物イオンが浸透しにくいように、拡散係数をコンクリートの1/10000としています。

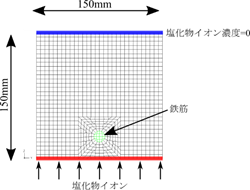
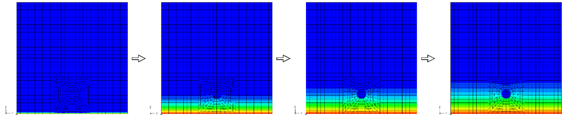
解析結果として塩化物イオン濃度のコンター図を示します。コンクリート内に塩化物イオンが拡散している様子を定性的に表現しています。拡散係数を小さく設定した鉄筋は塩化物イオン濃度が低くなっています。

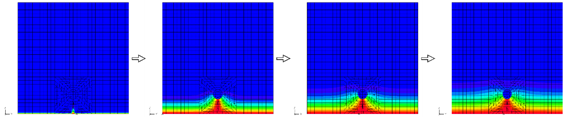
次に、コンクリートにひび割れが入っている場合を想定した拡散解析を行いました。コンクリート表面から鉄筋に向かってひび割れが入っていると仮定し、ひび割れ部分は水分や湿分を含む空隙となるので物質が拡散しやすいように拡散係数をコンクリートの1000倍としました。

拡散係数を大きく設定したひび割れ部分から塩化物イオンが浸透していく様子を再現しています。

おわりに

本記事では熱伝導解析プログラムを用いてコンクリート内部での塩化物イオンの非定常拡散解析を行いました。今回の解析は拡散現象を定性的に表現することに着目しており、拡散係数は厳密に設定したものではありません。定量的な評価を行う場合は、拡散係数をどう設定するかが重要になります。また、物質の移動には拡散だけでなく流れにより物質が運ばれる「移流」という現象もあり、拡散だけでなく移流も考慮する必要がある場合も多いです。

最後までお読みいただきありがとうございました。