数値解析による応答評価においては、安定性と精度の二つの観点から結果を評価することが重要である。このうち前者(安定性)においては、数値積分の条件設定に留意することでこれを解決することができる。
例えば、線形加速度法の安定条件は減衰を無視すると、系の固有円振動数を\(\omega\)とした場合、積分時間間隔\(\Delta t\)は以下の条件を満たすように設定することで安定性を確保できることが知られている。
\(\Delta t < \frac{2\sqrt{3}}{\omega} \)
しかしながら、構造解析においては減衰定数を設定することが一般的であり、減衰の値を大きくなると上式を満たすギリギリの \(\Delta t\) では解が発散してしまった経験はないだろうか。これは上式が減衰を無視するという仮定に基づいて算出された条件であり、減衰が無視できない場合においては減衰定数に関する項が安定条件に含まれるためである。
一般的な対処法としては、安定した解が得られるように \(\Delta t\) を小さく設定することが挙げられる。しかしながら、減衰がある場合に \(\Delta t\) が満たすべき条件を導出した事例は筆者の知る限り見当たらず、 \(\Delta t\) の設定が試行錯誤的になってしまっている現状がある。すなわち、本来であれば \(\Delta t\) を半分程度にすれば十分であるものを、1/10やそれ以下の値を設定してしまったがために計算時間が余計にかかってしまう、という状況が生まれてしまっている。
本コラムでは、陰解法の一種であるNewmark-β法を例にとり、減衰を無視しない場合における数値積分の安定条件を定量的に算出することを試みるものである。以降、運動方程式に数値積分を適用して安定条件を導出していくことになるが、その元となる運動方程式(1自由度系)を以下に示す。
\( m \ddot{x} + c \dot{x} + kx = P \) (1)
\(m\):質量、 \(c\): 減衰、 \(k\):剛性、 \(P\): 外力
(1)式の両辺を質量で除して離散化すると、あるステップにおける運動方程式は以下のように記述される。
\(\ddot{x}_n +2h\omega\dot{x}_n + \omega^2 x_n = f_n \) (2)
ただし、\( c/m=2h\omega \)、\(k/m=\omega^2 \) 、\(P/m=f_n \) 、\(h\)は減衰定数 、\(\omega \)は固有円振動数である。
Newmark-β法では、あるステップの速度および変位が以下の式で表現される。
\( \left\{ \begin{array}{l} \dot{x}_{n+1} = \dot{x}_n + \Delta t(1-\gamma)\ddot{x}_n + \Delta t \gamma \ddot{x}_{n+1} \\ x_{n+1} = x_n + \Delta t \dot{x}_n + \Delta t^2 (\frac{1}{2}-\beta)\ddot{x}_n + \Delta t^2 \beta \ddot{x}_{n+1} \end{array} \right. \) (3)
\(\beta,\gamma \):Newmark-β法の係数
\( \Delta t \):ステップ間隔
ここで、(2)式を\(\ddot{x}_n=\)の形に変形し、(3)式へ代入する。安定条件は自由振動状態の方程式に対して評価されるため、外力項=0でも差し支えないことを考慮すると、(3)式は以下のように記述される。
\( \left\{ \begin{array}{l} \dot{x}_{n+1} = \dot{x}_n + \Delta t(1-\gamma)(-2h\omega\dot{x}_n-\omega^2 x_n) + \Delta t \gamma (-2h\omega \dot{x}_{n+1}-\omega^2 x_{n+1}) \\ x_{n+1} = x_n + \Delta t \dot{x}_n + \Delta t^2 (\frac{1}{2}-\beta)(-2h\omega\dot{x}_n-\omega^2 x_n) + \Delta t^2 \beta (-2h\omega \dot{x}_{n+1} - \omega^2 x_{n+1}) \end{array} \right. \) (4)
(4)式は(5)式のようなマトリクス形式で表記でき、\( \left\{ X_n \right\}\)に関する漸化式と見なせることが分かる。
\( \left[ A \right] \left\{ X_{n+1} \right\} = \left[ B \right] \left\{ X_{n} \right\} \)
すなわち、
\( \left\{ X_{n+1} \right\} = \left[ A \right]^{-1} \left[ B \right] \left\{ X_{n} \right\} \) (5)
ただし、
\( \left[ A \right] = \left[ \begin{array}{cc} 1+2h\omega\gamma\Delta t & \omega^2\gamma\Delta t \\ 2h\omega\beta\Delta t^2 & 1+\omega^2\beta\Delta t^2 \end{array} \right] \)
\( \left[ B \right] = \left[ \begin{array}{cc} 1-2\Delta t(1-\gamma)h\omega & -\Delta t(1-\gamma)\omega^2 \\ \Delta t-2\Delta t^2(\frac{1}{2}-\beta)h\omega & 1-(\frac{1}{2}-\beta)\omega^2\Delta t^2 \end{array} \right] \)
\( \left\{ X_n \right\}= \left\{\begin{array}{l} \dot{x}_n \\ x_n \end{array}\right\} \)
ここで、\( \left[ A \right]^{-1} \left[ B \right] \)を計算すると、
\( \left[ A \right]^{-1} \left[ B \right] = \frac{1}{H} \left[ \begin{array}{cc} C_{11} & C_{12} \\ C_{21} & C_{22} \end{array} \right] \)
\(H=1+2h\omega\gamma\Delta t + \omega^2\beta\Delta t^2\)
\(C_{11} = 1-2h(1-\gamma)\omega\Delta t + (\beta-\gamma)\omega^2\Delta t^2 -h(2\beta-\gamma)\omega^3\Delta t^3 \)
\(C_{12} = -\omega^2\Delta t + (\frac{1}{2}\gamma-\beta)\omega^4\Delta t^3 \)
\(C_{21} =\Delta t + h(2\gamma-1)\omega\Delta t^2 + h^2(4\beta-2\gamma)\omega^2\Delta t^3 \)
\(C_{22} = 1+2h\gamma\omega\Delta t + (\beta - \frac{1}{2})\omega^2\Delta t^2 + h(2\beta-\gamma)\omega^3\Delta t^3 \)
(5)式が収束かつ振動解を持つ条件は、 \( \left[ A \right]^{-1} \left[ B \right] \) の固有値\(\lambda\)が複素数かつ大きさが1以下となるときである。
固有値\(\lambda\) は\(det | \left[ A \right]^{-1} \left[ B \right] -\lambda I |=0\)から得られる以下の特性方程式の解である。
\(\lambda^2 + \left[ -2+\frac{2h\omega\Delta t+(\gamma+\frac{1}{2})\omega^2\Delta t^2}{1+2h\gamma\omega\Delta t+\beta\omega^2\Delta t^2} \right]\lambda + 1 + \frac{(\frac{1}{2}-\gamma)\omega^2\Delta t^2 - 2h\omega\Delta t}{1+2h\gamma\omega\Delta t + \beta\omega^2\Delta t^2} =0 \) (6)
(6)式より、\(\lambda\)を下記の通り算出することができる。
\(\lambda = \frac{1}{2}\left[ 2-\frac{2h\omega\Delta t+(\gamma+\frac{1}{2})\omega^2\Delta t^2}{1+2h\gamma\omega\Delta t + \beta\omega^2\Delta t^2} \pm \sqrt{ \left\{ \frac{ 2h\omega\Delta t+(\gamma+\frac{1}{2})\omega^2\Delta t^2 }{ 1+2h\gamma\omega\Delta t + \beta\omega^2\Delta t^2 } \right\}^2 -\frac{4\omega^2\Delta t^2}{ 1+2h\gamma\omega\Delta t + \beta\omega^2\Delta t^2 } } \right] \)
\(\lambda\) が複素数となる条件は、
\( \left\{ \frac{ 2h\omega\Delta t+(\gamma+\frac{1}{2})\omega^2\Delta t^2 }{ 1+2h\gamma\omega\Delta t + \beta\omega^2\Delta t^2 } \right\}^2 -\frac{4\omega^2\Delta t^2}{ 1+2h\gamma\omega\Delta t + \beta\omega^2\Delta t^2 } <0 \)
であるから、式を以下のように変形すると\(\beta\)に関する条件が得られる。
\( 1+2h\gamma\omega\Delta t + \beta\omega^2\Delta t^2 > \left\{ \frac{ 2h\omega\Delta t+(\gamma+\frac{1}{2})\omega^2\Delta t^2 }{2\omega\Delta t} \right\}^2 = \left\{ h+\frac{1}{2}(\gamma+\frac{1}{2})\omega\Delta t \right\}^2 \)
\( \beta\omega^2\Delta t^2 > \frac{1}{4}(\gamma+\frac{1}{2})^2\omega^2\Delta t^2 -1+h^2+h(\frac{1}{2}-\gamma)\omega\Delta t \)
\( \beta > \frac{1}{4}(\gamma+\frac{1}{2})^2 - \frac{1}{\omega^2\Delta t^2} + \frac{h^2}{\omega^2\Delta t^2} + \frac{h(\frac{1}{2}-\gamma)}{\omega\Delta t} \) (7)
\( |\lambda| \leq 1 \)となる条件は、\(\lambda\)が複素数であることに注意すると、以下の式より導くことができる。
\(\lambda^2 = \frac{1}{4}\left[\left\{ 2-\frac{2h\omega\Delta t+(\gamma+\frac{1}{2})\omega^2\Delta t^2}{1+2h\gamma\omega\Delta t + \beta\omega^2\Delta t^2} \right\}^2 +\frac{4\omega^2\Delta t^2}{ 1+2h\gamma\omega\Delta t + \beta\omega^2\Delta t^2 } - \left\{\frac{ 2h\omega\Delta t+(\gamma+\frac{1}{2})\omega^2\Delta t^2 }{ 1+2h\gamma\omega\Delta t + \beta\omega^2\Delta t^2 } \right\}^2 \right] \\ = \frac{1}{4}\left[ 4-\frac{4\gamma\omega^2\Delta t^2}{ 1+2h\gamma\omega\Delta t + \beta\omega^2\Delta t^2 } +\frac{2\omega^2\Delta t^2-8h\omega\Delta t}{ 1+2h\gamma\omega\Delta t + \beta\omega^2\Delta t^2 } \right] \leq 1 \)
したがって、
\(\gamma \geq \frac{2\omega^2\Delta t^2-8h\omega\Delta t}{4\omega^2\Delta t^2} = \frac{1}{2}-\frac{2h}{\omega\Delta t} \) (8)
(7)(8)式より、計算が安定となる積分時間間隔\(\Delta t\)は、
\(\Delta t < \frac{h(2\gamma-1)+2\sqrt{(\gamma+\frac{1}{2})^2-4\beta+2h^2(2\beta-\gamma)} }{\omega \left\{ (\gamma+\frac{1}{2})^2-4\beta \right\} } \) (9)
\(\Delta t \leq \frac{2h}{\omega(\frac{1}{2}-\gamma)} \) (10)
と求められる。ただし、
\( (\gamma+\frac{1}{2})^2-4\beta+2h^2(2\beta-\gamma) >0\)
である。また、(10)式は(8)式より\(\gamma<\frac{1}{2}\)の範囲において満たすべき条件であり、\(\gamma\geq\frac{1}{2}\)の場合においては常に(8)式が成立する。(この場合、(10)式を評価することに意味はない)
さて、上記で導出した安定条件が正しいことを1自由度系の振動解析によって検証してみる。
振動系の諸元、解析条件を以下の通り設定し、応答加速度波形を確認する。
\(\omega=316.228 \)、\(\beta=\frac{1}{6} \)、\(\Delta t =0.01\)
Case1:\(\gamma=\frac{1}{2}\)、\(h=0\)
Case2:\(\gamma=0.494\)、\(h=0.01\)
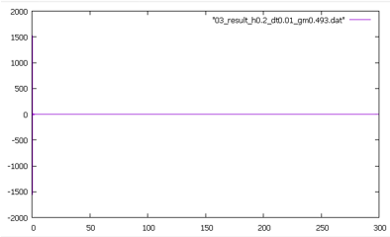
Case3:\(\gamma=0.493\)、\(h=0.01\)
Case4:\(\gamma=0.493\)、\(h=0.2\)
すべてのケースにおいて、入力する加速度は以下の図に示すパルス波形とする。
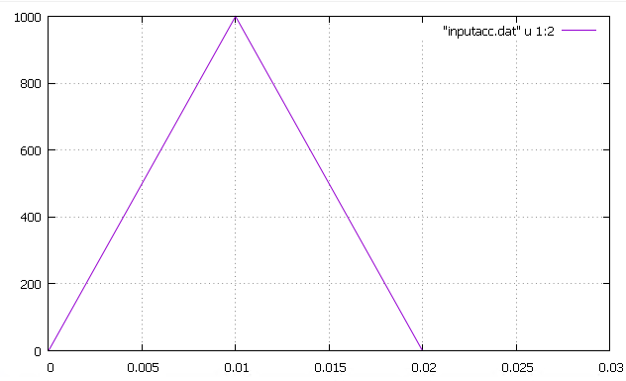
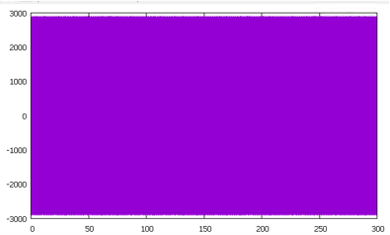
【Case1】
Case1は通常の線形加速度法となる条件である。したがって、応答加速度波形は以下に示す通り、発散も減衰もせず一定の振幅をとる。(系の固有振動数が非常に高いため、塗りつぶされたような図となってはいるが・・・)
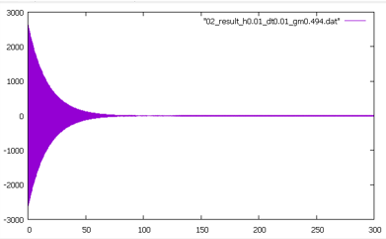
【Case2】
Case2は\(\gamma\)、\(h\)の値を少し変化させたケースであり、このときの安定条件は(9)(10)式から
\( \Delta t<0.01054\)
となる。解析は\(\Delta t =0.01\)として実施しており、安定条件を満たしているため応答加速度は以下に示すように減衰して収束することが確認できる。
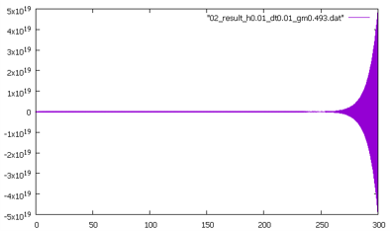
【Case3】
Case3はCase2から\(\gamma\)の値をわずかに変化させたケースであり、このときの安定条件は(9)(10)式から
\( \Delta t<0.00904\)
となる。解析は\(\Delta t =0.01\)として実施していることから、安定条件を満たさないため応答加速度は以下に示すように発散する。
【Case4】
Case4はCase3において\(h=0.2\)としたケースであり、このときの安定条件は(9)(10)式から
\( \Delta t<0.01094\)
となる。解析は\(\Delta t =0.01\)として実施しており、安定条件を満たしているため応答加速度は以下に示すように減衰して収束することが確認できる。(減衰の値が大きいため振動はすぐに収束する。縦軸の値はCase1,2と近い値である)
以上の通り、導出した安定条件の妥当性を数値解析によって検証することができた。
【補足】
ここで、減衰定数\(h\)=0のとき、(9)式は
\(\Delta t < \frac{2}{\omega \sqrt{ (\gamma+\frac{1}{2})^2-4\beta } } \)
となり、\(\gamma=1/2\)のとき、
\(\Delta t < \frac{2}{\omega \sqrt{ 1-4\beta} } \)
線形加速度法(\(\beta=1/6\))のとき、
\(\Delta t < \frac{2\sqrt{3}}{\omega } \)
であることがわかる。
また、(7)式において\(h=0\)とすると、
\(\beta > \frac{1}{4}(\gamma+\frac{1}{2})^2 -\frac{1}{\omega^2\Delta t^2} \)
となる。すなわち、よく用いられる平均加速度法(\( \beta=1/4,\gamma=1/2\))の係数の組み合わせにおいては\(\omega\)、\(\Delta t\)の値に関わらずこの関係を満たす(無条件安定)ことが分かる。
さらに、(8)式で等号が成立するとき、数値積分の過程においてエネルギーが保存される。一方、(8)式の等号が成立しないとき、系のエネルギーは減少することになる。


 (12 投票, 平均: 1.00 / 1)
(12 投票, 平均: 1.00 / 1)