AMDとは
建築構造におけるAMD(アクティブ・マス・ダンパー)とは、建物に応答制御用のマス(質量)を配置して、この動きを機械制御によりコントロールすることで建物自体の応答を低減させようとするものです。一方で、機械制御することなく、マスと建物の固有周期を同調させて応答低減を図るものをTMD(チューンド・マス・ダンパー)と呼びます。また、それらを組み合わせたものとしてHMD(ハイブリッド・マス・ダンパー)があります。
実装してみた
対象問題
建物の最上部に付加質量が設置されている構造を考えてみます。この付加質量を機械制御することで発生する制御力が建物に作用する問題を解きます。TMDやAMDは付加質量の大きさや設置の面から、一般的に風応答に対して居住性能向上を図る目的で使用されますが、ここでは外力として地震力を与えることとします。

AMDによる応答制御の概要
振動方程式
振動モデルの振動方程式は以下のように記述できます。通常の建物の振動方程式に制御力ベクトルが加わっているところがミソです。
\( [M] \{ \ddot x \} + [C] \{ \dot x \} + [K] \{ x \} =\{F\} + \{F_c\} \)
ここで、
\( [M] \) :質量マトリクス、 \( [C] \) :減衰マトリクス、 \( [K] \) :剛性マトリクス
\( \{F\} \) :外力ベクトル、 \( \{F_c\} \) :制御力ベクトル
\( \{ \ddot x \} \) :加速度ベクトル、 \( \{ \dot x \} \) :速度ベクトル、 \( \{ x \} \) :変位ベクトル
制御系
制御手法はいくつかありますが、ここでは比較的理解しやすいと思われる最適レギュレータ理論(LQR)を採用します。LQRで得られる制御は状態フィードバック制御(状態量にフィードバックゲインを掛けて制御力を計算する制御 )であり、以下の評価関数を最小化するフィードバックゲインを求めて、 制御力を振動方程式に考慮することで制御することになります。
\( J = \int(X^T QX + u^T Ru) \)
ここで、
\( X \) :状態量ベクトル、 \( u \) :制御力ベクトル
\( Q \) :状態量に対する重み行列、 \( R \) :制御力に対する重み行列
QとRは設計値であり、これらは大小関係だけに意味があります。例えば、Rに対してQが大きい場合、評価関数の第1項が大きくなることを抑えるためには、X(応答)を小さくする必要があり、そのためにはu(制御力)を大きくする必要があります。一方で、Qに対してRが大きい場合はその逆となります。つまり、これは状態量と制御力がトレードオフの関係にあることを意味します。QとRが決まれば、以下のRiccati方程式の解Pを用いてフィードバックゲインGが求められます。
\( Q-PBR^{-1} B^T P + PA + A^T P = O \)
\( G = -R^{-1}B^T P \)
ここで、
\( A = \left[ \begin{array}{cc} -M^{-1}K & -M^{-1}C \\ O & I \end{array} \right] \)
\( B = \left[ \begin{array}{cc} M^{-1}F \\ O \end{array} \right] \)
\( O \):零行列、 \( I \):単位行列
プログラミング言語
プログラミング言語にはJuliaを用いることにします。科学技術計算に向いており、MATLABライクにマトリクス演算が容易で、かつフリーに利用できるため、このようなプロトタイピングには向いていると思います。また、上記LQRによるフィードバックゲインを求めるライブラリがあるため、これを活用することで記述が簡単になります。Juliaについては以下の記事に詳細を記していますので是非ご参照ください。
https://kaiseki-kke.jp/blog/julia-eigen-1/
ソース
制御に関わる部分だけ記載します。ライブラリを利用することで以下のように簡単なコードで済みました。A、B、Q、Rをライブラリの関数に渡すだけでフィードバックゲインを取得できます。後は、ここで計算したフィードバックゲインGと状態量を掛け合わせて制御力を算出してこれを最初に示した振動方程式に考慮するだけです。
using ControlSystems function designFeedbackControlSystem(m_mat, k_mat, c_mat) Q = [ 1.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 0.0 1.0 0.0 0.0 0.0 0.0 0.0 ] r = 1.0*10^-9 A_lu = -1.0 * inv(m_mat) * c_mat A_ru = -1.0 * inv(m_mat) * k_mat A_ll = zeros(Float64, 2, 2) A_rl = ones(Float64, 2, 2) A = [ A_lu A_ru A_ll A_rl ] B_u = inv(m_mat) * [-1.0, 1.0] B_l = zeros(Float64, 2, 1) B = [ B_u B_l ] G = lqr(A, B, Q, r) return G end
結果
以下の図はAMDの有無で建物の速度応答にどのように差異が生じるか確認したものです。AMDを設置することで応答低減していることが確認できます。
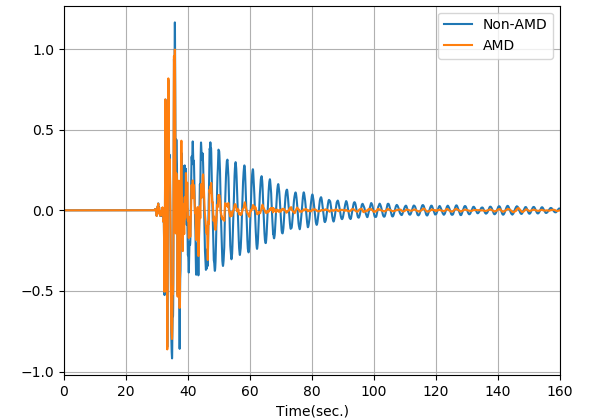
以下は応答変位アニメーションです。AMD有り(右)の方が応答が抑制されている様子が確認できます。※AMDの質点はここでは描画していません。

まとめ
LQR以外の制御や立体モデルへの応用はもう少し複雑ですが、問題を限定すれば 今回のように比較的簡単にAMDによる制御を実装できます。
参考文献
・日本建築学会『建築構造物の振動制御入門 INTRODUCTION TO VIBRATION CONTROL OF BUILDINGS 2010年』
・内野清士、富澤徹弥ほか、日本建築学会大会学術講演梗概集2012年9月『風力発電設備のアクティブ振動制御』



 (1 投票, 平均: 1.00 / 1)
(1 投票, 平均: 1.00 / 1)