Juliaとは?
プログラミング言語「Julia」とは、主に科学技術計算のために開発された比較的新しいプログラミング言語です。公式ホームページから抜粋すると、以下のような特徴を持ちます。
Juliaは、R、MATLABおよびPythonなどの言語と同様に、 高いレベルの計算処理における手軽さと見やすさを提供し、また一般的な プログラミングにも対応が可能です。
Julia公式ページ https://hshindo.github.io/julia-doc-ja-v0.6/manual/introduction.html
つまり、現在非常に世界的に人気の高い言語であるPythonのような書きやすさを持ちながら、行列演算で非常に強力な言語であるMATLABのような高度な行列演算機能を有する言語ということになります。加えて、以下のような特徴があることが個人的には非常に魅力的に感じました。
- コンパイル言語並みに高速に動作する。
- Pythonのライブラリを簡単に扱える。
つまり、言語としての使いやすさを追求するだけでなく高速な演算能力も両立し、豊富なライブラリによって人気を博しているPythonの資産も活用できる、まさに良いとこどりといえる言語です。
ただし、プログラミング言語は実際に使ってみないと真価はわかりません。そこで今回はまず固有値解析を題材にJuliaを使ってみたいと思います。
インストールする
インストールは公式サイトからインストーラをダウンロードできます。
公式サイト : https://julialang.org/
なお、インストールが自由にできる環境にない、もっと気軽に試したい、という方のために、ブラウザ上でコードを記述、実行、保存できるサービス「JuliaBox.com」が公式に用意されています。
JuliaBox : https://www.juliabox.com/
今回は上記のJuliaBoxを使ってみました。
行列演算を試してみる
まずはどの程度簡単に行列が使えるか試してみます。
まずは剛性マトリクス、外力ベクトルを用意して静的応力解析を行ってみます。以下のようなモデルを定義します。ソースコードは下記です。
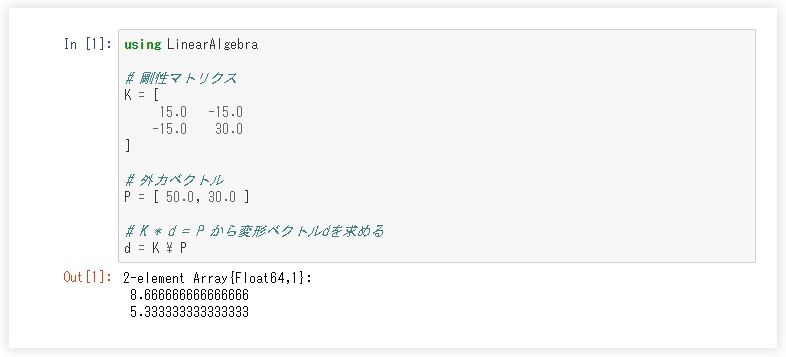
using LinearAlgebra # 剛性マトリクス K = [ 15.0 -15.0 -15.0 30.0 ] # 外力ベクトル P = [ 50.0, 30.0 ] # K * d = P から変形ベクトルdを求める d = K \ P
JuliaBoxでの実行結果は以下です。非常に簡単なコードで解が求まりました。特筆すべきは行列の可読性です。人間にも読みやすい形で記述することができます。
固有値解析を試してみる
もう少しだけ高度な解析として質点系振動モデルの固有値解析を例に固有値解析を行います。
固有値解析とは以下のような関係が成り立つ{u}≠{0}の解を求める計算になります。
\( ( -ω^2[M]+[K] ) \{u\} = \{0\} \)
ω : 固有円振動数, [M] : 質量マトリクス, [K] : 剛性マトリクス
まずは質点系振動モデルを作るための関数群を定義します。
# 線形代数ライブラリ using LinearAlgebra # 質点系の構造体 mutable struct LumpedMassModel size::Int64 m::Array{Float64, 1} c::Array{Float64, 1} k::Array{Float64, 1} LumpedMassModel() = new() end # 全体マトリクスに部分マトリクスを加算する # full : 全体マトリクス # part : 部分マトリクス # row, clm : 加算する位置(左上の行、列) function addToFullMatrix(full, part, row, clm) row_length = length(full[1, :]) clm_length = length(full[:, 1]) # rowが全体剛性マトリクスに含まれるか if 0 < row <= row_length # clmが全体剛性マトリクスに含まれるか if 0 < clm <= clm_length full[row, clm] += part[1, 1] end # clm + 1が全体剛性マトリクスに含まれるか if 0 < clm + 1 <= clm_length full[row, clm + 1] += part[1, 2] end end # row + 1が全体剛性マトリクスに含まれるか if 0 < row + 1 <= row_length # clmが全体剛性マトリクスに含まれるか if 0 < clm <= clm_length full[row + 1, clm] += part[2, 1] end # clm + 1が全体剛性マトリクスに含まれるか if 0 < clm + 1 <= clm_length full[row + 1, clm + 1] += part[2, 2] end end end # 質量マトリクスを作成する関数 function buildMassMatrix(model)::Array{Float64, 2} size = model.size mat = zeros(Float64, size, size) for index in 1:size mat[index, index] = model.m[index] end return mat end # 剛性マトリクスを作成する関数 function buildStiffnessMatrix(model)::Array{Float64, 2} size = model.size mat = zeros(Float64, size, size) for story_index in 1:size # 階のばね値を取得 k = model.k[story_index] # ばねの剛性マトリクスを構築 part = [ k -k -k k ] # 全体剛性マトリクスに加算 # 層間に配置するため、story_index - 1 ~ story_index の間 addToFullMatrix(mat, part, story_index - 1, story_index - 1) end return mat end
つづいて、これを使って5質点系モデルを作るコードです。
sample = LumpedMassModel() sample.size = 5 sample.m = [200.0, 200.0, 200.0, 200.0, 200.0] sample.k = [8000.0, 7000.0, 6000.0, 5000.0, 4000.0] mmat = buildMassMatrix(sample) kmat = buildStiffnessMatrix(sample) amat = kmat/mmat eigen_values = eigvals(amat) eigen_vector = eigvecs(amat) # 固有値はω^2なので、固有周期に変換する map(eigen_values) do omega2 2.0 * pi / (omega2 ^ 0.5) end
以下に実行結果を示します。固有周期が算出できました。
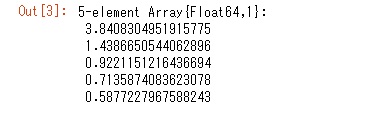
固有周期のほかに固有ベクトルも求まっています。Juliaには可視化ライブラリも用意されていますので、固有ベクトルを可視化してみます。ソースコードは以下です。
Pkg.add("Plots") using Plots function mode_values(eigen_vector, mode_index) eigvec1 = eigen_vector[:, mode_index] size = length(eigvec1) heights = [] push!(heights, 0.0) insert!(eigvec1, 1, 0.0) for index in 1:size push!(heights, float(index)) end return (eigvec1, heights) end function view_mode(eigen_vector, mode_index) (eigvec, heights) = mode_values(eigen_vector, mode_index) plot(eigvec, heights) end function view_modes(eigen_vector) size = length(eigen_vector[1, :]) mat_x = [] mat_y = [] for mode_index in 1:size (eigvec, heights) = mode_values(eigen_vector, mode_index) push!(mat_x, eigvec) push!(mat_y, heights) end plot(mat_x, mat_y) end view_modes(eigen_vector)
実行結果は以下です。
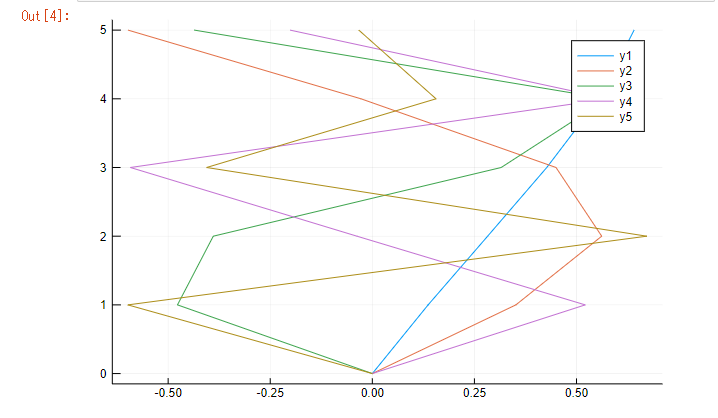
このように、行列の演算、可視化まで非常にスムーズに行うことができました。
まとめ
Juliaは科学技術計算向けプログラミング言語と称するだけあって、今回紹介した機能のほかにも多様な機能があります。その2では応用として、複素固有値解析の実装について書きたいと思います。



 (3 投票, 平均: 1.00 / 1)
(3 投票, 平均: 1.00 / 1)