弾性波探査におけるNMO補正手法の紹介

背景

　弾性波探査とは、地表面あるいは浅い地層で人工的に弾性波を発生させ、地層内の様々な経路を伝搬して地表に再到達した波形を分析することにより、地下構造を可視化する方法である。現在は地下資源（天然ガス、石油および石炭）の開発のみならず、海洋資源の採掘の分野でも広く使われている。

　今回は弾性波探査において、弾性波データの処理に必須のステップであるNMO補正手法について簡単に紹介する。

弾性波の概略

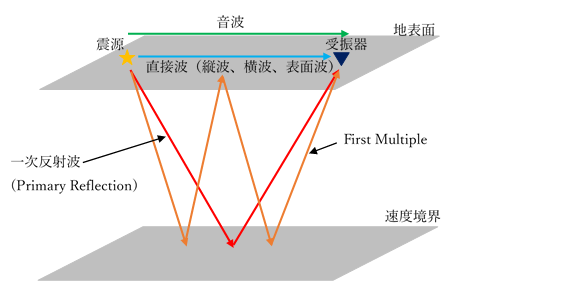
図-1 弾性波探査の測定方法の概要図

　弾性波とは弾性体に振動を加えたとき生成された波である。弾性波には、波の進行方向に平行に振動する縦波と、進行方向と直角に振動する横波と弾性体の表面を伝わる表面波（レイリー波及びラブ波）がある。

　人工震源（ハンマーや火薬等）で起振させた弾性波を用いて、密度と弾性波速度の積である音響インピーダンスの違う境界面を反射面として得ることにより、地下構造を明らかにするのが弾性波探査である。

　図-1に示した通り、まず震源から起振させた弾性波が地層と空気で伝播する。この波は地層で反射されずに直接受振器まで届くため直接波と呼ぶ。

　また、速度境界で一次反射されて受振器に届く波は一次反射波と呼ぶ。

　一方で、速度境界で多次反射された波はmultipleと呼ぶ。Multilpeは多次反射され、エネルギーが減少するため、波の振幅が小さいと考えられる。

データ処理の流れ

　受振器で獲得したデータを処理する際の前提条件を以下に示す 。
・震源と受信器が格子状の形で整列している（データの補間及び正則化のため）
・ 処理対象は縦波とする。他の波は雑音と扱われる 。
・ 多次反射された波は雑音と扱われる 。
また、弾性波のデータ処理の簡潔された流れは図-3で表示している。

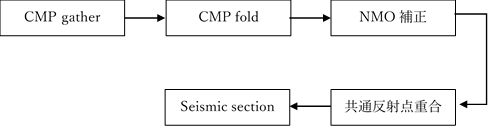
図-2 弾性波のデータ処理の流れ

　ここで、
CMP gatherとは弾性波探査における一つのデータ収集手法であり、同じ共通の地下の中点から一連の反射波を取得することである。すべての震源と受振器で構成された直線は測線と呼ばれている。

　CMP foldとは各受振器で獲得した弾性波のデータを時間-オフセットで示すことである。

　NMO補正とは、一つの測線で同一の反射点に対する獲得された波形を処理して、オフセットの影響を取り除くことである。

　共通反射点重合とは、前のNMO補正で修正された波形を加え合わせることである。単純に考えると、同一の反射点で得られた波形はほぼ同じである。一方で、ランダムな雑音波は不規則である。そこで反射点を共有する波形を加え合わせると、S/N比(信号/雑音比)が大幅に上がる。

　Seismic sectionとは、処理された多数の波形データを合成して表示することである。

NMO補正について

　実際の地層モデルは複雑であるため、簡単なモデルでNMO補正の原理を紹介する。

　図-3に示すような、単一の水平層モデルを想定する。Hは地層の深さ、Mはこの測線の中心点、Dは反射点、Snは震源、Rnは受振器、XnはSnとRnの間の距離（オフセット）、破線は縦波のトレースである。単一の地層なので、この地層における縦波の速度は一律でVとする。

　ピタゴラスの定理によると、

     　　  \(T^2=T_0^2+\frac{x^2}{v^2}\)                                       　　　　　 (1)

　計算式(1)から、下の計算式(2)が得られる：

     \(T=T_0\left(1+\frac{X^2}{v^2T_0^2}\right)\frac{1}{2}\) 　　                                    (2)

　ここに、\(T_0=2H/V\)

　そして、 NMO補正式は\(T\)と\(T_0\)の差で与えられる：

\(△T_{NMO}=T-T_0=T_0\left[\sqrt{1+\left(\frac{x}{V_{NMO}T_0}\right)^2} -1\right]\)              (3)

ここに、\(V_{NMO}\)は推測縦波の速度。

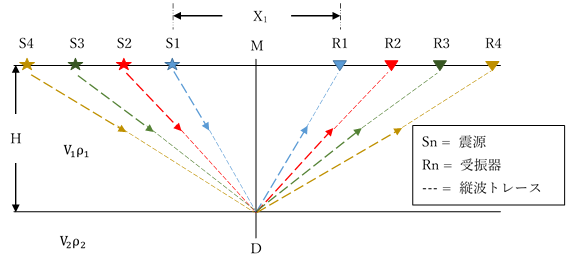
図-3 CMP測定方法の概念図

　なぜ、NMO補正が必要なのか？

　共通反射点を行って波形の質を高めるためには、その前に双曲線に沿って走時の違いを補正する必要がある。言い換えると、同じ反射点に対する異なる位置にある複数の受振器によって獲得した波形からオフセットの違いを取り去ると、同じ測線で得られた波形はほぼ同様になると考えられる。

NMO補正の数学的理論

　NMOの数学的理論の理解のため、この章では仮のデータ（X, T）を使って、関数グラフを描画してみた。

　もう一回計算式(1)を見ると、同じ測線で得られた波形データ(T, X)を図-5のようにT-X平面に描画した場合、双曲線の形で存在していると想像できる。実際にデータ処理する際には、オフセットX、走時Tと中心点にての走時T₀は既知であり、未知のパラメータは縦波の速度Vと地層の深さHである。ここで、得られた縦波の速度Vで計算式(3)の中のV_NMOを入れ替えるとΔT_NMOがわかる。このΔT_NMOによって図-4の双曲線を補正でき、波形データが垂直に上がって、水平の緑色破線に揃うようになる。

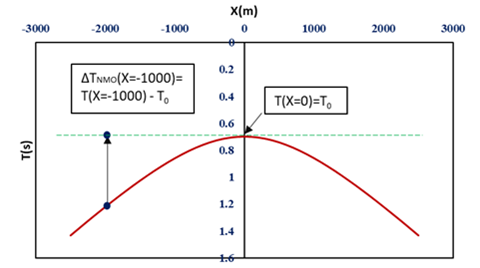
図-4 T-X平面におけるデータ（双曲線）

　 図-5の波形のデータをT²-X²の平面に描画してみた場合、これらのデータ群が線形近似で揃えていること（図-6）がわかった。計算式(1)から、

\(V=(slope)^{-1/2}\)                               (4)

                                   \(H=VT_0/2\)                                   (5)

　計算式(4)と(5)によると、この線形近似の勾配と切片の値が知れば、VとHとの値が解ける。

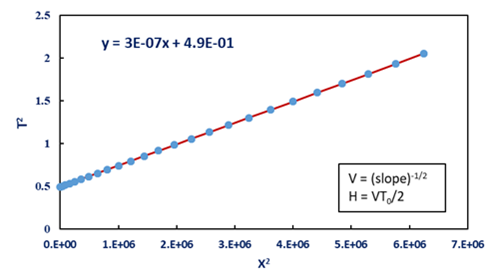
図-5 T²-X²におけるデータ（線形）

　ただし、実際のデータ処理においては、いつもきれいで、ちゃんと揃っている線形データ群が獲得できるわけではない。図-6に示した通り、高品質の波形データでは、よいV_NMOの値が得られ、適宜NMO補正ができる(図6-b)。ところが、低品質の波形データでは、実速度と異なる速度が得られる可能性がある。算定された速度が実速度より遅い場合には過補正という現象が起き（図6-c）、実速度より速い場合には欠補正という現象が起きる（図6-d）。

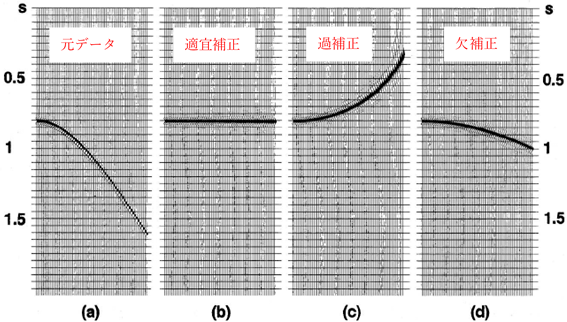
(a)元CMPデータV_NMO=2264m/s, (b) 適宜V_NMOで補正された波形, (c) V_{NMO =} 2000m/sで補正された波形, (d)V_{NMO =} 2500m/sで補正された波形.

図-6 異なる速度で行ったNMO補正

まとめ

　適宜NMO補正された波形データに基づいて弾性波探査を行うことにより、横軸が距離、縦軸が波の反射時間である反射時間断面図を作成できる。また、反射時間断面図を縦軸が深度である反射深度断面図に変換する際に、弾性波速度に関する情報が必須である。エネルギーが強い震源によって、探査深度が数kmの反射深度断面図も得られる。地球物理研究者たちはこれらの図面を判読したうえで、地下資源や海洋資源等の存在を推定できる。