斜め梁に作用する分布荷重の支点反力計算

１．はじめに

１スパンの単純梁に対し、水平梁の鉛直方向に分布荷重が作用する場合（図１）の反力や変位などは公式として広く認知されている。しかしながら、図２のように、傾斜した梁に鉛直分布荷重が作用する問題となるとすぐに答えの導き方をイメージできる人は多くない印象を受ける。そこで、まずは支点反力の導出方法を紹介する。

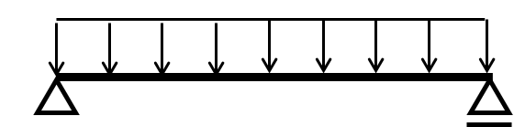
図１ 単純梁に対する分布荷重の入力

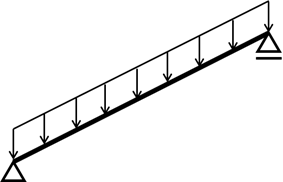
図２ 斜め梁に対する分布荷重の入力

２． 作用荷重の分解による方法

評価対象とする問題を図２のように設定した。梁は長さを$c$とし、傾きを$θ$とすると$tanθ=\frac{b}{a}$となる角度で設置されている。この梁に分布荷重$w$が鉛直下向きに作用するときの、支点$A$の反力を導出する。

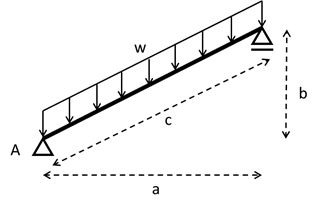
図２ 対象とする問題

作用荷重を梁軸直角方向と梁軸平行方向に分解すると、図３の通りとなる。あとは、支点$A$の梁軸直交方向の反力を$V_A$、梁軸平行方向の反力を$H_A$とすると、それぞれの反力は以下の通り計算される。

$V_A= \frac{1}{2}\times{w}\cos\theta\times{c}$
$H_A= \frac{1}{2}\times{w}\sin\theta\times{c}$

※可動支持は水平には動くが、斜めには動かないので２方向の反力が発生する。

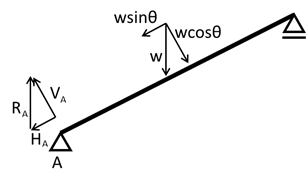
図３ 作用荷重の分解

したがって、荷重作用方向の反力$R_A$は以下のように求められる。

$R_A＝\sqrt{V_A^2+H_A^2} =\frac{1}{2}wc$

３． 仮想変位の原理による方法

別のアプローチとして、仮想変位の原理を適用した求め方を示す。仮想変位の原理とはごく単純に言えば、エネルギーのつり合いから力学的なつり合いを求める方法である。

例えば、図４に示すような単純梁の支点反力を求める問題を仮想仕事の原理を用いて導出する場合には、反力を求めたい支点に仮想変位$Δ=1$を与えたとき（図５）のエネルギーを計算し、つり合いを求める。微小変位の仮定において、つり合いを表現する計算式は以下の通りである。

$P×\frac{1}{2}+R×1=0$

すなわち、

$R=-\frac{p}{2}$ (上向きに$\frac{p}{2}$)

となる。

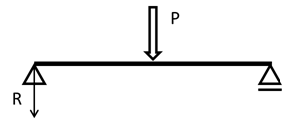
図４ 単純梁への載荷問題

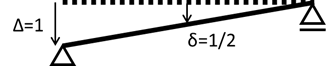
図５ 仮想変位を与えたときの梁の変形状態

図２の梁に仮想変位を与えたときの梁の変形状態は図６の通りとなる。なお、梁の軸方向を$x$軸と設定している。

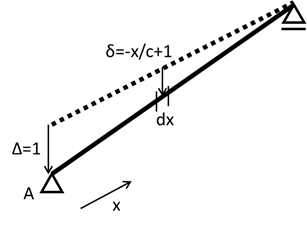
図６ 仮想変位を与えたときの梁の変形状態

これをもとに、仮想変位の原理を定式化すると以下の通りとなる。

$\int_0^c w\left( -\frac{x}{c}+1 \right) dx-R_A\times1=0$

ゆえに、本式を解くと荷重作用方向の反力が以下のように直接算出される。

$R_A=\frac{1}{2}wc$

なお、実務では分布荷重が風圧や水圧であることが多く、梁軸方向の荷重が無視できる場合が多い。その際には梁軸方向分の荷重を差し引いて計算を行わなければならない点に留意が必要である。