前回の記事
その1の記事では、科学技術計算向けスクリプト言語Juliaを用いて固有値解析を行いました。
https://kaiseki-kke.jp/blog/julia-eigen-1/
今回は減衰項の影響も考慮した固有値解析である複素固有値解析を行ってみたいと思います。
複素固有値解析とは?
その1で説明した固有値解析では、減衰マトリクスは考慮しないものとしてましたが、減衰マトリクスを考慮した固有値解析が複素固有値解析です。固有値解析の解が実数で求まるのに対し、複素固有値解析の解は複素数で求まることから、計算および結果の評価が難しくなります。その一方で、 各モードの減衰定数が計算されるためダンパーの効果について定量的に評価できるなど、通常の固有値解析では得られないメリットもあります。
複素固有値解析の実装
減衰項が入った場合の振動方程式は以下のようになります。
\( [M] \{ \ddot x \} + [C] \{ \dot x \} + [K]x=0 \)
おさらいですが、固有値解析とは[A]{x}=λ{x}となるような解を求めることです。速度は変位の1階微分、加速度は変位の2階微分であることを利用すると、上記の式は以下のように記述できます。
\(-ω^2 [M] \{ \ddot x \} +ω [C] \{ \dot x \} + [K]\{x\}=0 \)
ここで、[C]=[O]である通常の固有値解析であれば、以下の形に変換できます。
\([M]^{-1}[K]\{x\}=ω^2\{x\} \)
上記はまさに [A]{x}=λ{x} の形ですので、通常の固有値解析であればこの形で固有値解析が行えます。しかしながら、[C]の項が入るとこのままでは [A]{x}=λ{x} の形にすることができません。そこで、{x}を用いて以下のような{X}を定義します。
\( {X}=\{\{ x \},\{ \dot x\}\} \)
そうすると、先の振動方程式を以下のように書きなおすことができます。
\( [A] = [ \)
\(\qquad \qquad [O] \qquad \qquad [O] \)
\( \qquad [M]^{-1}[K] \qquad [M]^{-1}[C] \)
\( ] \)
\( [A]\{ X \} = \{ \dot X \} = \omega^{2} \{ X \} \)
この形であれば [A]{X}=λ{X} の形となっていますので、固有値解析を行えば解を求めることができます。なお、[C]を含む場合には計算される固有値は複素数で算出されます。算出された解の実部、虚部は以下のような意味を持つため、そこから固有値、減衰定数を逆算することになります。
実部 : \( -h × \omega \)
虚部 : \( \sqrt{ (1-h^2) } × \omega \)
h : 減衰定数, ω : 固有円振動数
プログラム
複素固有値解析を行うサンプルプログラムを記載します。
using LinearAlgebra M=[ 3.0 0.0 0.0 3.0 ] C=[ 20.0 -20.0 -20.0 40.0 ] K=[ 50.0 -50.0 -50.0 100.0 ] O=zeros(Float64, 2, 2) I=[ 1 0 0 1 ] A= [ O I -M\K -M\C ] # 固有値の取得 vals = eigvals(A) # 1次固有円振動数 # 周期が長い = 振動数が小さい値 omega = abs(vals[4]) T = 2.0 * pi / omega # 減衰定数を取得 h = - real(vals[4]) / omega
実行結果を一つずつ追っていきます。
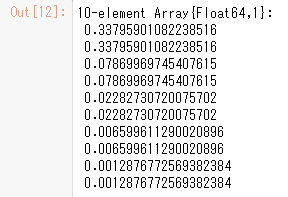
まず、固有値解析を実行して固有値を取得すると以下のような解が求まります。
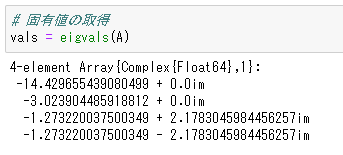
振動数が小さい値が1次固有周期となるため、4つ目の値を取り、固有周期、減衰定数を算出します。

5質点モデルの計算結果
もう少し実践的な5質点系モデルで実際に複素固有値解析を行ってみました。前回の記事で作成したソースコードを使って、免震構造を模擬する質点系モデルにダッシュポットを入れて複素固有値解析を行ってみます。
モデル諸元は以下の通りです。
| 階 | 質量(t) | 剛性(kN/m) |
| 5 | 600 | 300000 |
| 4 | 600 | 300000 |
| 3 | 600 | 300000 |
| 2 | 600 | 300000 |
| 1 | 800 | 10000 |
1次固有周期は3.617秒、1次の固有モードは以下のような形状です。
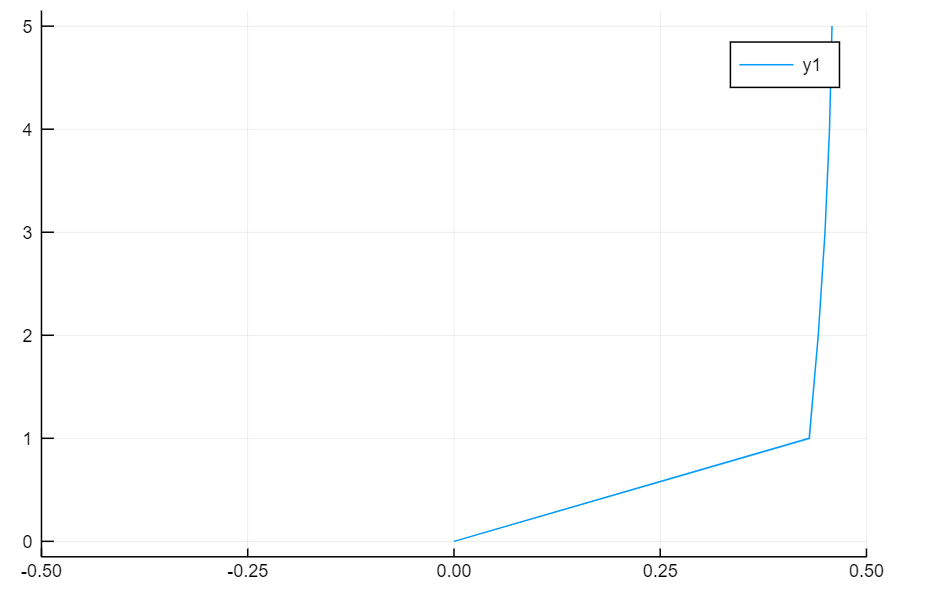
免震層に 1000kN/(m/s)~4000kN/(m/s)の減衰係数を持つダンパーを入れた場合の固有周期、減衰定数の変化を確認します。
コードは以下の通りです。
using LinearAlgebra # 質点系の構造体 mutable struct LumpedMassModel size::Int64 m::Array{Float64, 1} c::Array{Float64, 1} k::Array{Float64, 1} LumpedMassModel() = new() end # 全体マトリクスに部分マトリクスを加算する # full : 全体マトリクス # part : 部分マトリクス # row, clm : 加算する位置(左上の行、列) function addToFullMatrix(full, part, row, clm) row_length = length(full[1, :]) clm_length = length(full[:, 1]) # rowが全体剛性マトリクスに含まれるか if 0 < row <= row_length # clmが全体剛性マトリクスに含まれるか if 0 < clm <= clm_length full[row, clm] += part[1, 1] end # clm + 1が全体剛性マトリクスに含まれるか if 0 < clm + 1 <= clm_length full[row, clm + 1] += part[1, 2] end end # row + 1が全体剛性マトリクスに含まれるか if 0 < row + 1 <= row_length # clmが全体剛性マトリクスに含まれるか if 0 < clm <= clm_length full[row + 1, clm] += part[2, 1] end # clm + 1が全体剛性マトリクスに含まれるか if 0 abs(x), vals))[2] push!(results, vals[target_index]) end
固有周期、減衰定数変化の結果を示します。
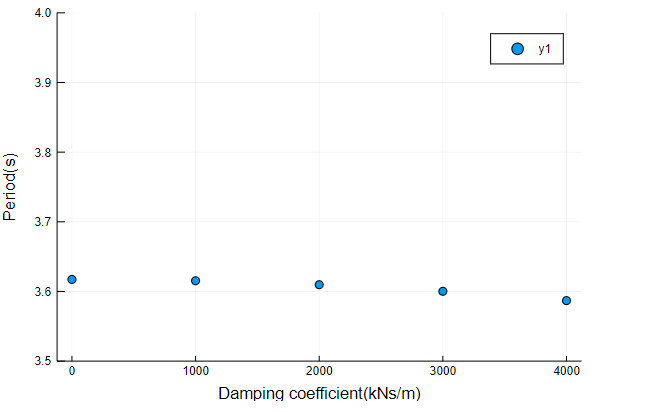
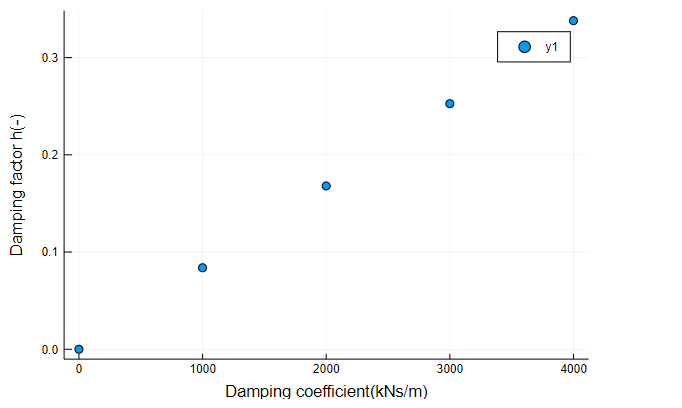
1次固有周期は3.617秒~3.587秒、減衰定数は約10%~30%程度まで変化しました。今回は非常に単純なモデルでしたが、複素固有値解析では系としての減衰定数が求まるため、ダンパーの最適配置などにも活用の可能性があります。
RESPとの比較
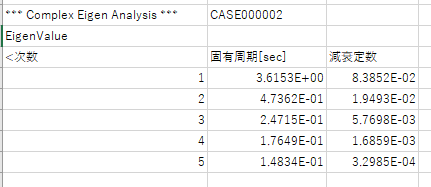
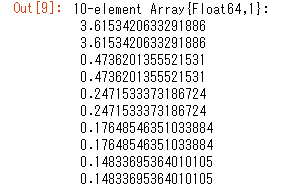
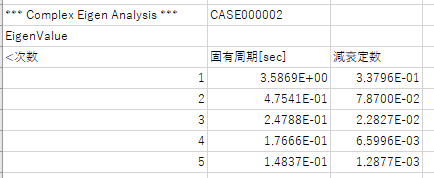
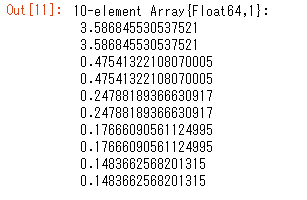
当社の汎用構造解析プログラムRESP-F3Tの結果と比較してみます。ダンパーは 1000kN/(m/s) , 4000kN/(m/s) のものを配置してみます。
当然ですが、結果がよく一致することが確認できました。Juliaでは行列のサイズを倍にして作っているため、結果が二つずつでています。

まとめ
今回はjuliaで複素固有値解析を行ってみました。手軽に複素固有値解析が行えるツールは多くなく、これまで個人的にも複素固有値解析は敬遠していましたが、juliaであれば非常に手軽に扱えることがわかりました。ぜひ機会があればご活用ください。



 (まだ評価がありません)
(まだ評価がありません)