- はじめに
- 検討対象モデルおよび解析条件
- 解析結果
- まとめ
数値解析において、「ばね」はとても身近なものである。バネ-マス系、地盤ばね、接触ばねなど、様々な「ばね」が用いられている。一般に、数値解析における「ばね」はこんな感じで表現し、押したり引っ張ったりしている。

図1 数値解析における一般的な「ばね」
しかしながら、通常、ばねと言えばこういうものである。

図2 いわゆる通常のばね
そこで、図2のようなばねを数値解析において圧縮してみた。(引っ張るのは簡単なので今回は割愛)
今回作成したモデルを図3に示す。ばねは圧縮コイルばねを対象とし、線径0.5mm、コイル平均径20mm、自由長さ120mm、有効巻数15の少々大きめのばねを想定した。ばねは三次元梁要素でモデル化しているため、ばねに作用する軸力、せん断力、モーメント、ねじりなどを表現することができる。なお、材料物性は弾性としている。
解析はモデルの一端を固定し、反対側に変位を静的に与える方法により実施した。解析コードは「LS-DYNA」を使用している。
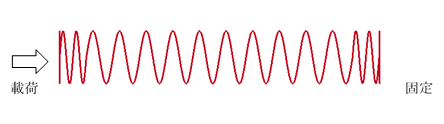
図3 解析モデル
解析結果を図4~図6に示す。図中、赤色の線が実際のばねの変形であり、水色の線は載荷前のばねの位置である。これらの図より、載荷直後はほぼ水平にばねが変形しているものの、載荷が進むと固定端付近からばねが座屈し、荷重載荷方向と直交する方向への変形が発生していることが確認できる。
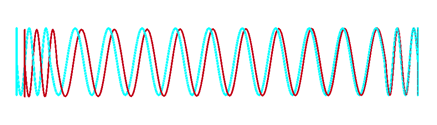
図4 載荷直後
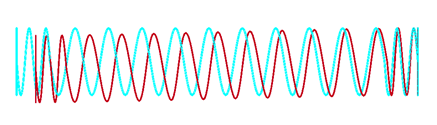
図5 載荷継続中
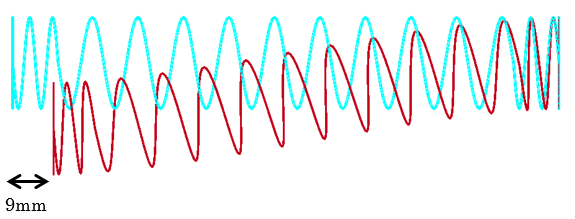
図6 解析終了時
なお、線径を3mmとした場合においても、 同様に変位を与えると座屈が発生した。
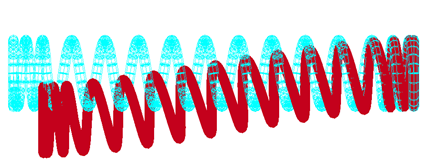
図7 線径3mmとした場合の変形状態
ばねの形状をそのままモデル化して圧縮力をかける解析を実施した。その結果、座屈を発生させずに押し切ることは難しいことが分かった。設定したばねの長さや、圧縮方向以外の自由度を拘束していないことなど、数値解析における「ばね」の仮定とは異なる部分が多いものによることが考えられる。
図2のようなばねの両端を手で押して圧縮する場合は両端固定とみなせ、たいていの場合はばねの中央で座屈してしまう。今回の解析条件は片持ち形式であり、両端固定のばねを中央で切断した形となることから、荷重載荷点で座屈が発生している現象は実現象に対応していると判断できる。


 (10 投票, 平均: 1.00 / 1)
(10 投票, 平均: 1.00 / 1)